最大と最小
こんにちは
何卒宜しくお願い致します。
Re: 最大と最小
 管理人
管理人  2023/02/10(Fri) 01:07 No.55
2023/02/10(Fri) 01:07 No.55
こんばんは。
あっしの手には負えないので、
知恵袋からの引用と少し付けたし
00年東大文系
f(x,y)=1-ax-by-axy
fをxの関数と見れば高々1次式(一次関数).
よって,最小になりうるのはx=-1 or 1のとき.
fをyの関数と見れば,高々1次式(一次関数).
よって,最小になりうるのはx=-1 or 1のとき.
よって,-1≦x≦1,-1≦y≦1 におけるf(x,y)の
最小値の候補は
f(-1,-1),f(-1,1),f(1,-1),f(1,1)しかなく,
これらがすべて正であることが必要十分.
f(-1,-1)=b+1>0
f(-1,1)=1+2a-b>0
f(1,-1)=1+b>0
f(1,1)=1-2a-b>0
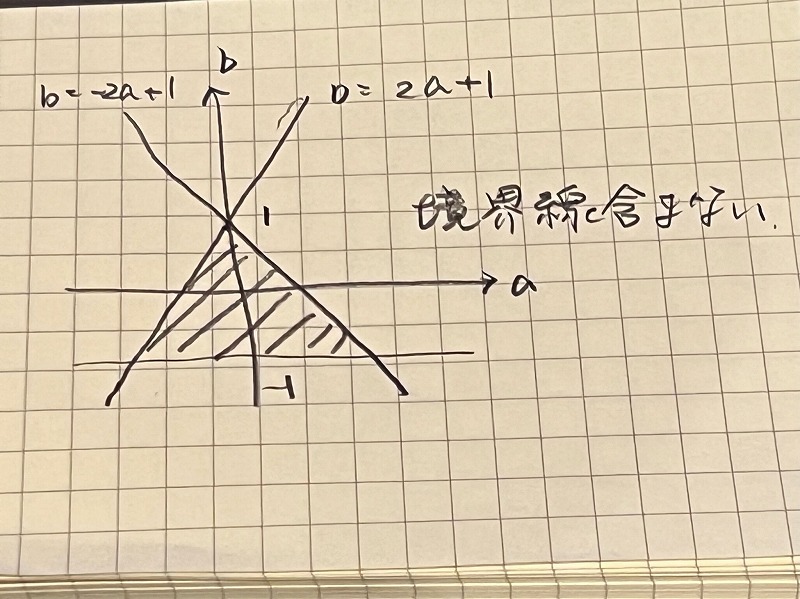
以上より,-1<b かつ b<-2a+1 かつ b<2a+1
リンク
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1452773619?fr=sc_scdd&__ysp=eHnlubPpnaLjga7poJjln58gLTHiiaZ4IDEtYXgtYnktYXh5
あっしの手には負えないので、
知恵袋からの引用と少し付けたし
00年東大文系
f(x,y)=1-ax-by-axy
fをxの関数と見れば高々1次式(一次関数).
よって,最小になりうるのはx=-1 or 1のとき.
fをyの関数と見れば,高々1次式(一次関数).
よって,最小になりうるのはx=-1 or 1のとき.
よって,-1≦x≦1,-1≦y≦1 におけるf(x,y)の
最小値の候補は
f(-1,-1),f(-1,1),f(1,-1),f(1,1)しかなく,
これらがすべて正であることが必要十分.
f(-1,-1)=b+1>0
f(-1,1)=1+2a-b>0
f(1,-1)=1+b>0
f(1,1)=1-2a-b>0
以上より,-1<b かつ b<-2a+1 かつ b<2a+1
リンク
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1452773619?fr=sc_scdd&__ysp=eHnlubPpnaLjga7poJjln58gLTHiiaZ4IDEtYXgtYnktYXh5
 管理人
管理人  2023/02/10(Fri) 01:07 No.55
2023/02/10(Fri) 01:07 No.55