emathソースコード：円の接線と弦のつくる角度の問題

こんにちは。相城です。

数Aの円の接線と弦のつくる角度の問題です。以下の図の問題ができます。emathのソースコードはその下に置いております。外接円(Gaisin)を駆使していけばできると思います。

emathのソースコードは以下のようです。

%Copyright Keiji Aiki　数学問題提供サイト数樂
\documentclass[fleqn,leqno,11pt,a4j]{jarticle}
\usepackage{graphicx}
\usepackage{emathPs}
\usepackage{emathPh}
\usepackage{emathEy}
\usepackage{fancyhdr}
\pagestyle{fancy}
\lhead{}
\rhead{}
\cfoot{\thepage} 
\rfoot{数樂　http://www.mathtext.info/} 
\renewcommand{\headrulewidth}{0pt}
\begin{document}
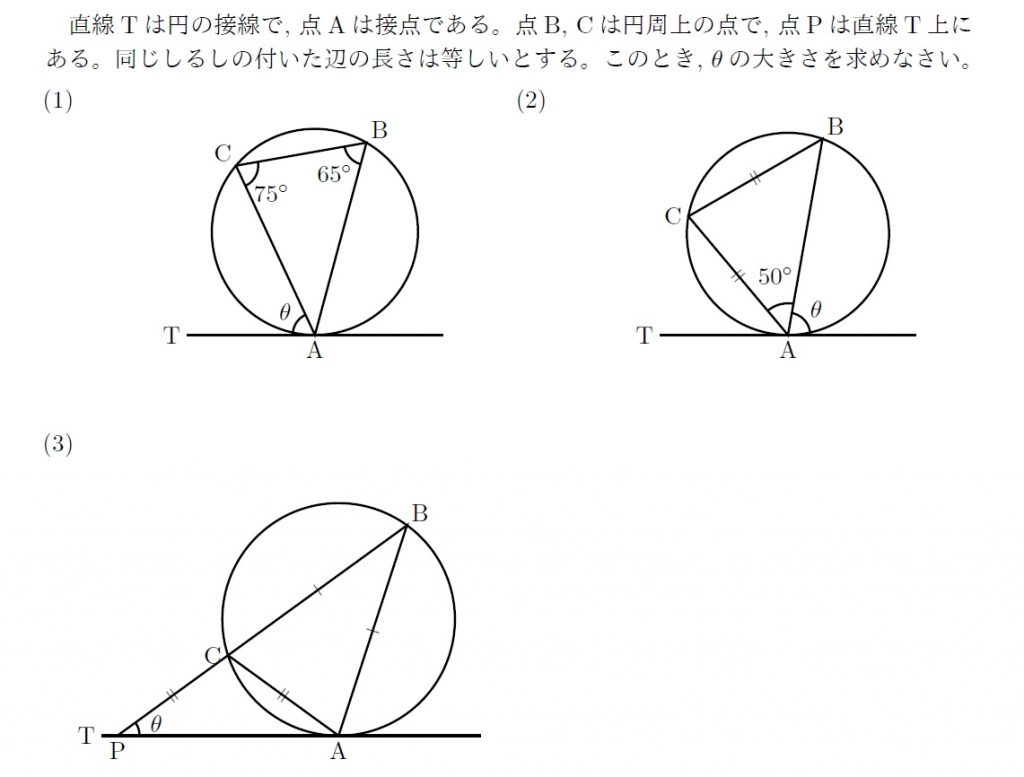
直線Tは円の接線で, 点Aは接点である。点B, Cは円周上の点で, 点Pは直線T上にある。
同じしるしの付いた辺の長さは等しいとする。このとき, $\theta$の大きさを求めなさい。
\begin{edaenumerate}[(1)]
\item
\begin{pszahyou*}[haiti=t,ul=4.5mm,Hidariyohaku=2.5mm,Sitayohaku=3mm](-3,13.5)(-2.5,8)
\tenretu{T(0,0)w;A(4.5,0)s}
\tenretu*{TT(9,0)}
\Candk\A{7}\A{75}\P\B
\Put\B[ne]{B}
\kandk\B{10}\A{115}\C
\Put\C[nw]{C}
\Gaisin\A\B\C\O
\Takakkei{\A\B\C}
\Drawline{\T\TT}
\En\O\lR
\Kakukigou\C\A\T(-5pt,5pt){$\theta$}
\Kakukigou\A\C\B(7pt,-8pt){75$\Deg$}
\Kakukigou\C\B\A(-7pt,-7pt){65$\Deg$}
\end{pszahyou*}
\item
\begin{pszahyou*}[haiti=t,ul=4.5mm,Hidariyohaku=2.5mm,Sitayohaku=3mm](-3,13.5)(-2.5,8)
\tenretu{T(0,0)w;A(4.5,0)s}
\tenretu*{TT(9,0)}
\Candk\A{7}\A{80}\P\B
\Put\B[ne]{B}
\kandk\A{130}\B{30}\C
\Put\C[w]{C}
\Takakkei{\A\B\C}
\Drawline{\T\TT}
\Gaisin\A\B\C\O
\En\O\lR
\Kakukigou\TT\A\B(5pt,5pt){$\theta$}
\Kakukigou\B\A\C<Hankei=5mm>(-2pt,13pt){50$\Deg$}
\touhenkigou<kosuu=2>{\B\C;\A\C}
\end{pszahyou*}
\item
\begin{pszahyou*}[haiti=t,ul=5mm,Hidariyohaku=2.5mm,Sitayohaku=3mm](-3,13.5)(-2.5,9)
\tenretu{T(-3,0)w;A(4.5,0)s}
\tenretu*{TT(9,0)}
\Candk\A{7}\A{72}\P\B
\Put\B[ne]{B}
\kandk\B{36}\A{144}\C
\Put\C[w]{C}
\Gaisin\A\B\C\O
\Takakkei{\A\B\C}
\Drawline{\T\TT}
\En\O\lR
\LandL\C\B\T\TT\P
\Put\P[s]{P}
\Drawline{\C\P}
\Kakukigou\A\P\C(8pt,2.5pt){$\theta$}
\touhenkigou<kosuu=2>{\C\P;\A\C}
\touhenkigou{\A\B;\B\C}
\end{pszahyou*}
\end{edaenumerate}
\end{document}