こんにちは。相城です。
こちらの記事に天才数学者が二次方程式の簡単な解き方を考案!「推測も暗記も必要ない」とあったので, さっそく一般化してみた結果, 二次方程式の解の公式が出てきたのでご報告。・・・至極当たり前のことなので, あっそれ俺も気づいてたってのも承知しております。
それでは記事の解き方というものをこちらでもご紹介。一般的な二次方程式の解き方で因数分解から考える問題の場合, 積の部分から考えるのが一般的なやり方です。以下の問題の場合積が12で和が![]() になる数字を考えるのですが, なぜ積から考えるかというと, 積の方が有限個数で決まるから。もちろん整数で考えた場合ですが。この天才数学者の発想は逆のようで和から考えてるんだと推察いたします。では以下の問いを参考に見てまいりましょう。
になる数字を考えるのですが, なぜ積から考えるかというと, 積の方が有限個数で決まるから。もちろん整数で考えた場合ですが。この天才数学者の発想は逆のようで和から考えてるんだと推察いたします。では以下の問いを参考に見てまいりましょう。
![]() という二次方程式があったとします。
という二次方程式があったとします。
ここで![]() の係数の
の係数の![]() の部分の符号を変えた8に注目して足して8になる数字を考えたとします。それを8の半分の4と4を基とします。このとき, 足して8になる数字は無限に考えられます。こんな風に
の部分の符号を変えた8に注目して足して8になる数字を考えたとします。それを8の半分の4と4を基とします。このとき, 足して8になる数字は無限に考えられます。こんな風に
![]() ,
, ![]() (この2数の和は8)
(この2数の和は8)![]()
掛け算して12になる数字を考えるのですが, この2数をかけると12になるので次の式が成り立ちます。![]()
展開すると![]()
![]()
これを![]() に代入すると6, 2が得られます。これが二次方程式
に代入すると6, 2が得られます。これが二次方程式![]() の解になります。
の解になります。
まぁこんな感じですね。そこでこの解き方を使って, 一般解を求めることに挑戦しました。以下インスタの写真とTwitterから。
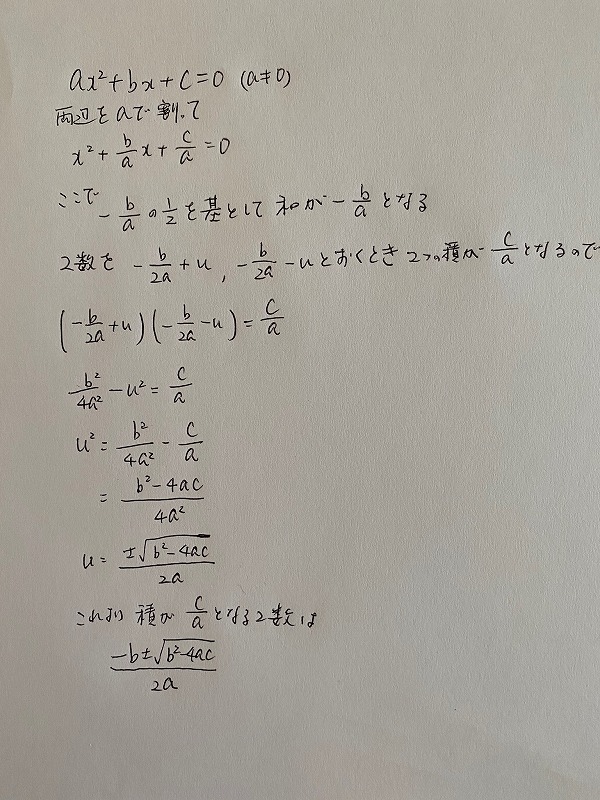
結局こう言うことですな。 https://t.co/W0HmBZa78y pic.twitter.com/2zkntvPjZy
— 沢庵 (数学講師)相城啓志 (@mathtext) December 29, 2019
 数樂管理人のブログ
数樂管理人のブログ 

