こんにちは。相城です。
前回複素数の積は回転という話をしましたが、その延長にあるドモアブルの定理をご紹介します。これ知っておくと三角関数の3倍角の定理が覚えなくても済む?のでご紹介します。意外と便利ですのでどうぞ。
どんな定理かというと以下のような定理です。
ドモアブルの定理:![]()
さて、これを証明するのは帰納法を使うといいですね。
ドモアブルの定理の証明
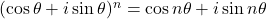 として、
として、
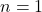 のとき
のとき
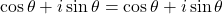
で成り立つ。
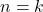 のとき、
のとき、
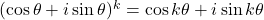 が成り立つとすると、
が成り立つとすると、
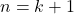 において
において
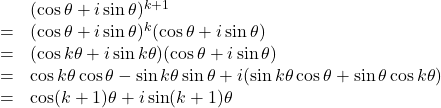
となり、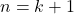 でも成り立つ。したがってすべての自然数
でも成り立つ。したがってすべての自然数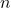 について成り立つ。
について成り立つ。
よって,
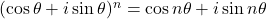
で成り立つ。
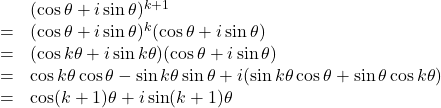
となり、
よって,
さて、初めに書いた3倍角の定理を覚えなくていいというのが、この定理で![]() として展開するとどうでしょう。
として展開するとどうでしょう。
ここで便宜上、ドモアブルの定理の左辺と右辺を入れ替えて展開するのですが、このとき、右辺の3乗の展開を一般的な展開公式を用いて展開します。以下にそれを示しています。
3倍角の公式の導出
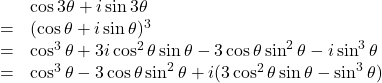
このとき、左辺と右辺の実部と虚部は恒等的な関係なので、
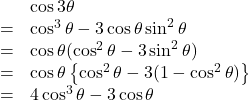
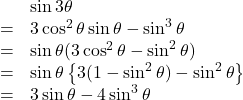
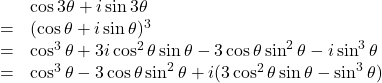
このとき、左辺と右辺の実部と虚部は恒等的な関係なので、
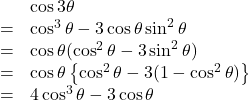
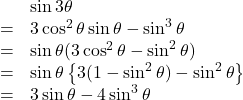
このように、実数部と虚数部を比較することで、3倍角の公式が得られます。このことは、![]() を適当に決めることで
を適当に決めることで![]() 倍角の公式が得られることを意味します。いいでしょ? 2倍角の定理なんか試しに求めてもいいよね。
倍角の公式が得られることを意味します。いいでしょ? 2倍角の定理なんか試しに求めてもいいよね。
これ覚えとくと困ったときに便利というか覚える公式が減る。公式なんて覚えられる人が覚えればいいんですよ。現地調達でも時間足りるような勉強しよう。
 数樂管理人のブログ
数樂管理人のブログ 

