こんにちは。相城です。さて、2020年度入試から神奈川県の最短距離の問題をピックアップ。解答は最後を除いて選択形式ですが、あえて選択形式にはしておりません。それでは面白い問題ですのでどうぞ。
図の五角形ABCDEはある三角すいの展開図であり、AB![]() BC
BC![]() CD
CD![]() DE
DE![]() EA
EA![]() 6cm、
6cm、![]() である。
である。
また、点Fは線分BCの中点であり、2点G、Hはそれぞれ線分AF、DFの中点である。
この展開図を3点B、C、Eが重なるように組み立てたときの三角すいについて、次の問いに答えなさい。
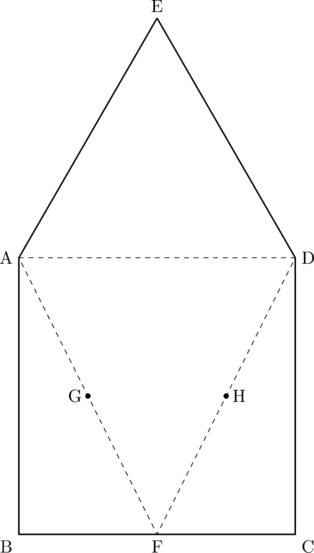
(1) この三角すいの表面積を求めなさい。
(2) この三角すいの体積を求めなさい。
(3) 3点B、C、Eが重なった点をIとする。この三角すいの表面上に、点Gから辺AI、辺DIと交わるように点Hまで、長さが最も短くなるように線を引いたときの線の長さを求めなさい。

答え
(1)
1辺が6cmの正三角形と1辺6cmの正方形の面積の和。
よって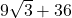 cm
cm
(2)
組み立てると底面が正三角形ADEで高さがBF CF
CF 3cmの三角すいになる。よって求める体積は、
3cmの三角すいになる。よって求める体積は、
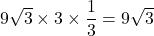
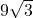 cm
cm
(3)
1辺が6cmの正三角形と1辺6cmの正方形の面積の和。
よって
(2)
組み立てると底面が正三角形ADEで高さがBF
(3)

求めるのは上図の赤線の長さ。
AD![]() 6で、上の図でFF
6で、上の図でFF![]() の長さが求まれば中点連結定理でDHの長さが求まることに着眼する。
の長さが求まれば中点連結定理でDHの長さが求まることに着眼する。![]() となる。△IFF
となる。△IFF![]() は頂角120
は頂角120![]() の二等辺三角形で、長さの等しい2辺はそれぞれ3cmです。頂点IからFF
の二等辺三角形で、長さの等しい2辺はそれぞれ3cmです。頂点IからFF![]() に垂線IKを下ろして、△IKFを見ると、30
に垂線IKを下ろして、△IKFを見ると、30![]() 、60
、60![]() 、90
、90![]() の直角三角形(
の直角三角形(![]() )になっているので、KI
)になっているので、KI![]() 、KF
、KF![]() となる。したがって、FF
となる。したがって、FF![]() KF
KF![]() 。よって、求めるGHの長さはAD
。よって、求めるGHの長さはAD![]() とFF
とFF![]() の和となる。ゆえに、GH
の和となる。ゆえに、GH![]() cm,または
cm,または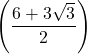 cm
cm
 数樂管理人のブログ
数樂管理人のブログ 

