TikZ：2020年度栃木県・三平方の定理の基本

こんにちは。相城です。2020年3月に栃木県で行われた高校入試の問題より、中3レベルの基本問題をお届けします。それではどうぞ。

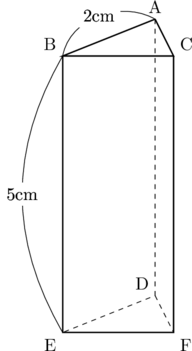
下の図は、1辺が2cmの正三角形を底面とする高さ5cmの正三角柱ABC－DEFである。
(1) 正三角形ABCの面積を求めなさい。
(2) 辺BE上にBG＝2cmとなる点Gをとる。また、辺CF上にFH＝2cmとなる点Hをとる。
このとき、△AGHの面積を求めなさい。

答え

(1) 1辺が2cmの正三角形の面積は
底辺2、高さ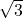 $\sqrt{3}$ なので、
求める面積は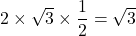 $2\times\sqrt{3}\times\dfrac{1}{2}=\sqrt{3}$
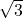$\sqrt{3}$ cm $^2$
(2)

Rendered by QuickLaTeX.com

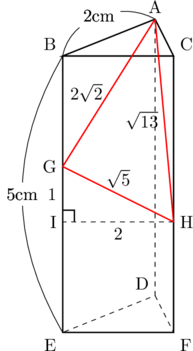
△ABG、△ACH、△HGI(HIはEFに平行にひいた線分)において、それぞれ三平方の定理を用いて、線分AG、AH、GHをそれぞれ求めると、AG＝ $2\sqrt{2}$ 、AH＝ $\sqrt{13}$ 、GH＝ $\sqrt{5}$ となる。単位は略。△AGHを抜き出して以下に示す。

Rendered by QuickLaTeX.com

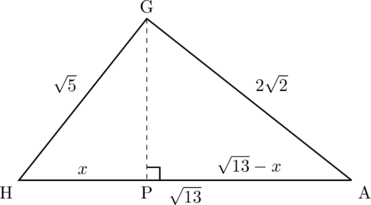
上記のようにGからAHに垂線GPを下ろしてGPを求めてもよいが、・・・よく見ると、三平方の定理(GH $^2$ ＋AG $^2$ ＝AH $^2$ )が成り立ちます。つまり△AGHは直角三角形です。気づきましたか？
$(\sqrt{5})^2+(2\sqrt{2})^2=(\sqrt{13})^2$
よって $\angle{\text{AGH}}$ ＝90 $^{\circ}$
したがって、求める面積は
$\sqrt{5}\times2\sqrt{2}\times\dfrac{1}{2}=\sqrt{10}$
$\sqrt{10}$ cm $^2$
ちなみに上図の $x$ は $x=\dfrac{2\sqrt{10}}{\sqrt{13}}=\dfrac{2\sqrt{130}}{13}$

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル