こんにちは。相城です。さて今回は2020年3月に徳島県で行われた高校入試の数学の問題より関数と図形の問題をピックアップ。それではどうぞ。
下の図のように, 2つの関数![]() と
と![]() のグラフが,
のグラフが, ![]() 座標が
座標が![]() である点Aで交わっている。直線OAと, 関数
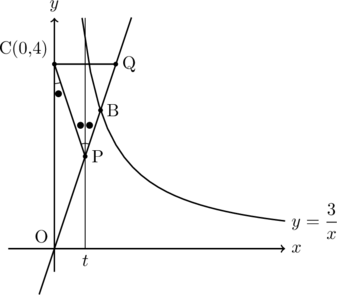
である点Aで交わっている。直線OAと, 関数![]() のグラフとの交点のうち, 点Aと異なる点をBとする。また, 点Cの座標は(0, 4)であり, 点Pは線分OB上の点である。(1)~(4)に答えなさい。
のグラフとの交点のうち, 点Aと異なる点をBとする。また, 点Cの座標は(0, 4)であり, 点Pは線分OB上の点である。(1)~(4)に答えなさい。
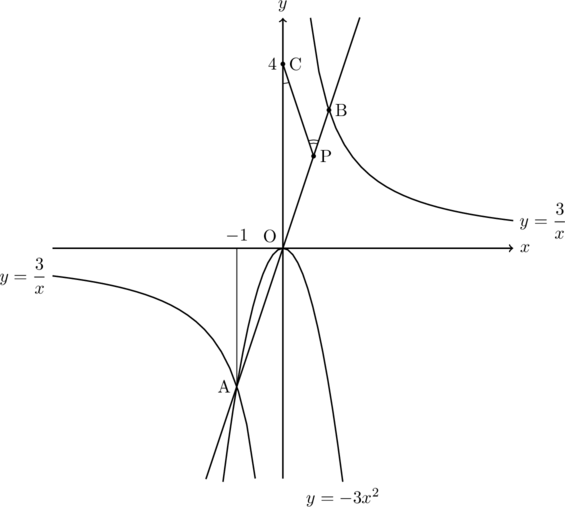
(1) 点Aの![]() 座標を求めなさい。
座標を求めなさい。
(2) 関数![]() について,
について, ![]() の変域が
の変域が![]() のときの
のときの![]() の変域を求めなさい。
の変域を求めなさい。
(3) 点Pが線分OBの中点のとき, 2点C, Pを通る直線の式を求めなさい。
(4) ![]() のとき, 点Pの座標を求めなさい。
のとき, 点Pの座標を求めなさい。

答え
(1) 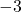
(2)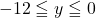
(3) A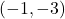 より, B(1, 3)であるから, 線分OBの中点の座標は
より, B(1, 3)であるから, 線分OBの中点の座標は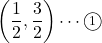 。
。
求める直線の式は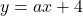 とおけるので, これに
とおけるので, これに を代入し
を代入し を求めると,
を求めると, 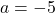
よって, 求める直線の式は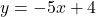
(4) 点Cを通る 軸に平行な直線と, 直線直線OBの交点をQとするとき, △PCQが二等辺三角形になればよい。このとき△PCQの頂角
軸に平行な直線と, 直線直線OBの交点をQとするとき, △PCQが二等辺三角形になればよい。このとき△PCQの頂角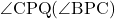 は
は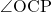 の2倍になる。
の2倍になる。
Pの 座標を
座標を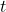 とすると点Qの
とすると点Qの 座標は
座標は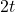 となるので, Qの座標はQ
となるので, Qの座標はQ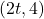 となる。この点Qが直線OB(
となる。この点Qが直線OB(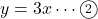 )上にあるので,
)上にあるので,  の式に点Qの座標を代入すると,
の式に点Qの座標を代入すると,
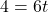 ,
,
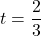
よって求めるPの 座標は
座標は なので, これを
なので, これを の式に代入し,
の式に代入し, 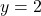 。よって, P
。よって, P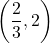
(2)
(3) A
求める直線の式は
よって, 求める直線の式は
(4) 点Cを通る
Pの
よって求めるPの
この解法も参照ください。
△PCOがPC![]() POの二等辺三角形になれば, 問題の条件は満たす。このとき, Pの
POの二等辺三角形になれば, 問題の条件は満たす。このとき, Pの![]() 座標はCOの中点になるので, Pの
座標はCOの中点になるので, Pの![]() 座標は2である。これを
座標は2である。これを![]() に代入し,
に代入し, ![]() ,
, ![]() として,
として,
P![]() を得る。
を得る。
 数樂管理人のブログ
数樂管理人のブログ 


三角形PCOが二等辺三角形として求めるのもアリですね!
ありがとうございます。
なるほどです。
答に追記しておきます。