TikZ：2020年度徳島県・こんなところに連立方程式の問題が

こんにちは。相城です。2020年度の徳島県の高校入試の問題に粋な計らいがあったので、報告いたします。今回の数学の問題において連立方程式の文章問題がないと思ったのですが, 実は最後の図形問題にそれが隠されていたというお話です。

徳島県の問題

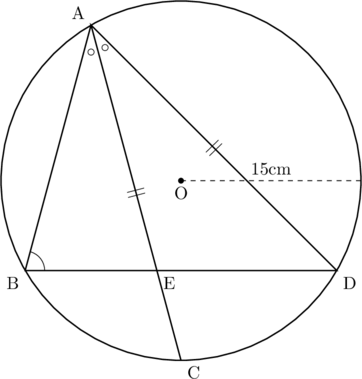
下の図のように, 半径が15cmの円Oの周上に4点A, $\$ B, $\$ C, $\$ Dがあり, AC $=$ ADである。また, 弦ACは $\angle{\text{BAD}}$ の二等分線であり, 弦ACと弦BDの交点をEとする。(1)～(3)に答えなさい。ただし, 円周率は $\pi$ とします。
(1) $\angle{\text{BAD}}=80^{\circ}$ のとき, (a), (b)に答えなさい。
(a) $\angle{\text{ABD}}$ の大きさを求めなさい。
(b) 点Aを含まないおうぎ形OBCの面積を求めなさい。
(2) △ABC $\equiv$ △AEDを証明しなさい。
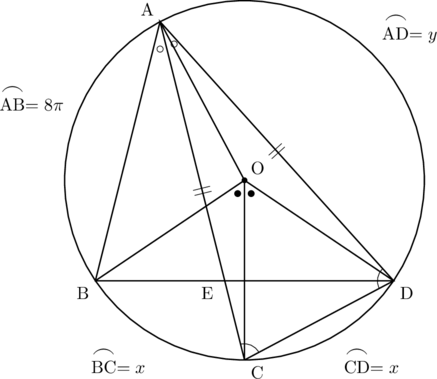
(3) 点Cを含まない $\arc{\text{AB}}$ の長さが $8\pi$ cmのとき, 点Bを含まない弧ADの長さを求めなさい。

この問題の(3)なんですが、連立方程式で解けますね。以下にそれを書きました。

$\angle{\text{BAC}}=\angle{\text{CAD}}$ なので, $\angle{\text{BOC}}=\angle{\text{COD}}$ 。このことより,
$\arc{\text{BC}}=\arc{\text{CD}}$ となる。ここで $\arc{\text{BC}}=x$ cm, $\arc{\text{CD}}=x$ cm, $\arc{\text{AD}}=y$ cmとおくと, $\arc{\text{AB}}=8\pi$ cmで, この円の円周は $30\pi$ cmなので, $2x+y+8\pi=30\pi$ となり,
$2x+y=22\pi\cdots\maru1$
また, △ACDは二等辺三角形なので, $\angle{\text{ADC}}=\angle{\text{ACD}}$ となり, $\arc{\text{AC}}=\arc{\text{AD}}$ だから,
$8\pi+x=y\cdots\maru2$
$\maru1, \maru2$ を連立方程式として解くと,
$x=\dfrac{14}{3}\pi$ , $y=\dfrac{38}{3}\pi$
よって、求める長さは, $\dfrac{38}{3}\pi$ cm