こんにちは。相城です。さて, 疑問解消の糸口を見ていきまでょう。
最近はあまり聞かれなくなりましたが, なぜ割り算を掛け算に直すと,
![]()
になるのでしょうか。具体例を挙げて説明します。
まず, ![]() ですね。
ですね。
ここで割られる数字100と割る数字10に同じ数字を掛けても答えは変わらないのをご存じでしょう。つまりこういうことです。
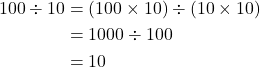
この理屈を分数の割り算などでも使っているのです。
先ほどの理屈通り, 割られる数字
すると,
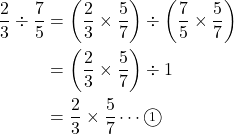
もとの式と
文字で置き換えると,
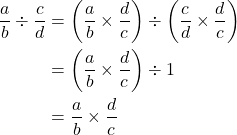
となります。
 数樂管理人のブログ
数樂管理人のブログ 

