中学数学：自転車に学ぶ反比例(関数)

こんにちは。相城です。身近な題材をテーマに反比例を見ていきましょう。

自転車に学ぶ反比例(関数)

自転車に学ぶ歯車のかみ合い。

自転車のギアって, 前と後ろにあってチェーンで結ばれて, かみ合っています。
ギア比ってのがあって, ギア比は1回ペダルを回す(前のギアを1回転する)ときに, 何回後ろのギアが回転するかを表したものです。
　(ギア比)(前のギアの歯数) (後ろのギアの歯数)
で求まります。ギア比が大きいと高速走行が可能になります。ギア比が小さいと登り坂などが楽に登れます。
ギア比の話はこれでおしまいにして, 本題へ移りましょう。

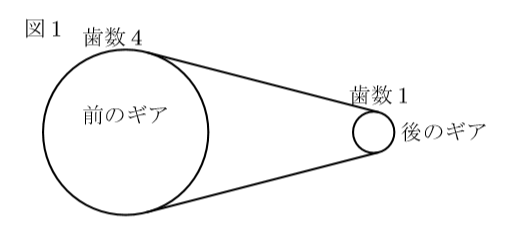
図1の略図では, 分かりやすくするために, 前のギアの歯数を4, 後の歯数を1としました。このとき, 前のギアが1回転するとき, つまり, 歯が414動くとき,
それに併せて, 後ろのギアも4動こうとします。これは歯がかみ合っているからです。しかし, 後ろのギアの歯は1つしかないので, 4回回らなければいけません。
したがって, 上の図から, 前のギアを1回転させると後ろのギアは, 4回転することが分かります。1回で4回回そうとするのですから, ペダルをこぐときは, 重たく感じます。
これがペダルの重さの原因です。ではギアを前後同じにするとどうでしょう。

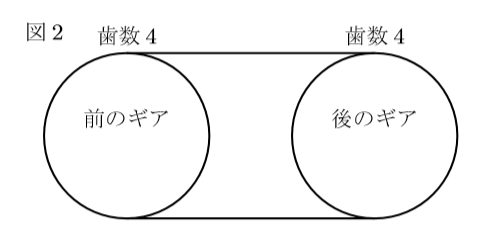
図2の略図では, 前後のギアの歯数が同じですから, 前のギアが1回転すると, 後ろのギアは1回しか回りません。ですから, 図1のものと比べると, 図1では1回転で4回転するのに対し, こちらは, 1回転で1回転ですから, 図1と同じ距離を進むためには4倍ペダルをこがなくてはいけません。
しかし, ペダルの重さは図1に比べると軽いです。抵抗が小さくなるからです。
私自身,抵抗なんて物理的なことはよくわかりませんが, 負担が少なくなるのは, なんとなくわかります。

いま, 歯車Aと歯車Bがかみ合っていて, 回転しているとします。
歯車がかみ合う問題では,

(歯車Aの歯数)(歯車Aの回転数)(歯車Bの歯数)(歯車Bの回転数)

が成り立ちます。これは歯車がかみ合っているから, 1度に動く歯の数が歯車Aと歯車Bで等しくなるからです。図1で実験してみれても, 理解できるはずです。
歯車の問題は, 古臭い問題ですが, 中学受験ではちらちら出題されているようです。公立高校入試でもあまり見かけない問題ですが, テーマが身近なだけに出題されるかもです。
この関係式は, 反比例の問題として出題されることが多いですが, 比例の問題としても出題可能ですので, その辺は気を付けていきましょう。