中学数学：本当の投影図

こんにちは。相城です。投影図について研究してみましょう。

真ん中の線は基線

まず投影図について, 立面図と平面図の間に引いてある線を 基線と言います。2つの投影面の交わりを意味します。
さて, 下の投影図からは円錐が想像できます。これは皆さん大丈夫ですよね。

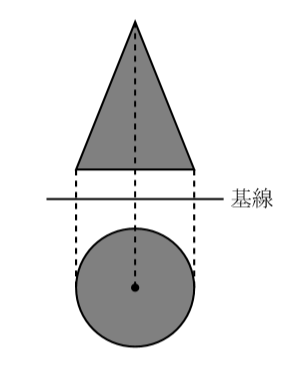
では下の図のような, 平面図と立面図が合同な長方形の投影図の場合, あなたはこの立体を何だと考えますか。

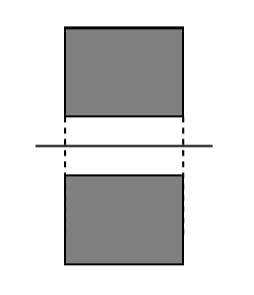
A君は正四角柱(直方体)と答えました。しかし, B君は円柱と答えました。そして, Cさんは 三角柱と答えました。まだ, 考えれば何か出てきそうですが, この3つの意見を聞いて, どう思いますか? 実はこれらは全部正しい意見なのです。A君の正四角柱は納得していただけるかもしれませんが, B君, C君は投影図を見てどのような発想から, 円柱や三角柱といった意見を述べたのでしょうか。

B君・C君の思考

B君とC君の考え方を, 下に示しました。これを見ると確かに, 正四角柱ではなく, 円柱にも三角柱にも見えますよね。

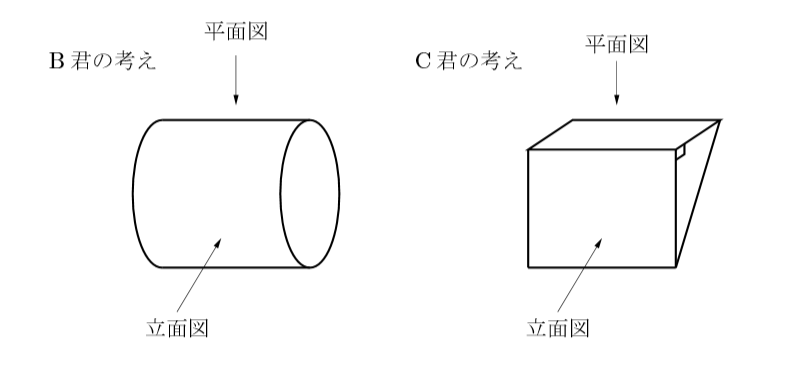
つまり, 立面図と平面図だけの投影図だけでは, 何の立体なのか正しく判断できないことがあるんです。
そのため登場するのが, 側面図です。

第三角法

そして, 立面図, 平面図, 側面図の3つを合わせたものを第三角法(正式名称は恥ずかしながら, 最近知りました。)と言います。この投影法は機械分野では重要な投影法で知られています。 私自身, 機械加工の分野で働いていたこともありまして, 少しぐらいは記憶に残っています。 話はそれましたが, では第三角法を使うとどんな投影図になるのでしょうか。見てみましょう。
先ほどのB君の考え方を例にすると

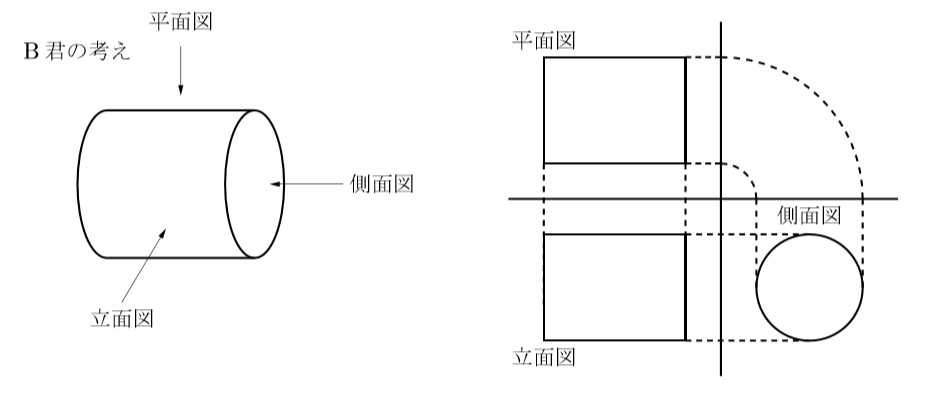
この図を見てわかるように, 中学生で習う投影図と立面図と平面図の位置が逆になっていますね。 これでないとC君の考え方が表わせないんです。下の投影図をご覧ください。左のは何かおかしいですよね。

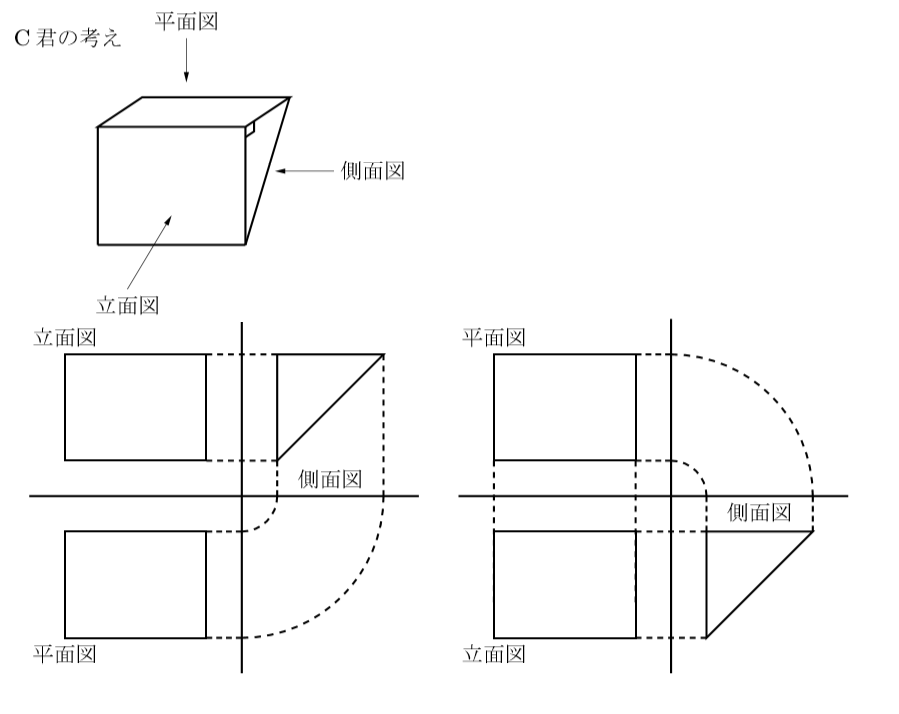
先の左の図は直角二等辺三角形の斜辺の部分が, 平面図の部分に対応してしまっている。
しかし, 平面図と立面図を入れ替えた右の図では, ものの見事に平面図が直角二等辺三角形の直角をはさむ辺と対応できているのが分かる。中学校ではここまでの厳密性は必要ないですが, 将来図面を広げるような職業に就くときは, しっかり製図の方法や図面の見方を勉強したいものです。ではでは。

プリントアウト用pdf