こんにちは。相城です。円錐関連の公式の導出を書いておきます。単純に公式を暗記するのではなく, 覚えられる方は理屈も確認しておきましょう。
円錐の公式の導き方
円錐の展開図において, 側面のおうぎ形の半径(円錐の母線)を![]() ,
,
側面のおうぎ形の弧の長さ(底面の円の周の長さ)を![]() , おうぎ形の中心角を
, おうぎ形の中心角を![]() , 円錐の側面積(おうぎ形の面積)を
, 円錐の側面積(おうぎ形の面積)を![]() , 底面の円の半径を
, 底面の円の半径を![]() とする。
とする。
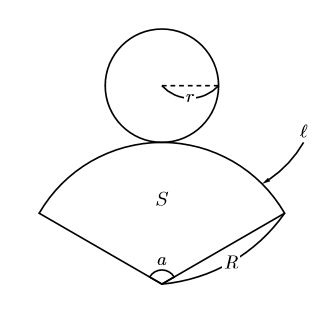
側面の扇形の弧の長さ![]()
![]()
側面の扇形の面積
![]()
![]()
![]()
下線部は
![]()
これより,
![]()
また
![]()
![]()
![]()
![]()
よって,
![]()
まとめ
まとめ:円錐関連の公式
- 円錐の側面積
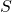 の公式
の公式
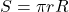
- 円錐の表面積
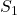 の公式
の公式
(表面積) (側面積)
(側面積)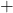 (底面積)
(底面積)
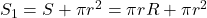
- 側面のおうぎ形の中心角

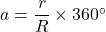
![]() に関しては
に関しては![]() という公式があるが, 登場は
という公式があるが, 登場は![]() の方が使用頻度は高いと思われるので割愛している。では例題をやってみよう。
の方が使用頻度は高いと思われるので割愛している。では例題をやってみよう。
例題をやってみよう
下の図のような円すいの展開図がある。側面の展開図は, 半径が6cm, 中心角が
![]() のおうぎ形で, 底面の円の半径は4cmである。このとき, (1), (2)の問いに答えなさい。ただし, 円周率は
のおうぎ形で, 底面の円の半径は4cmである。このとき, (1), (2)の問いに答えなさい。ただし, 円周率は![]() とする。
とする。
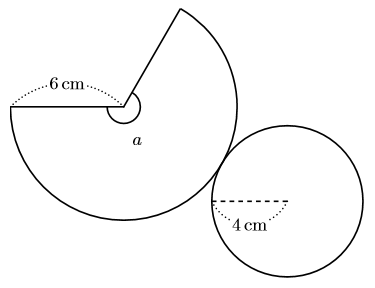
(1) 側面のおうぎ形の中心角![]() の大きさを求めなさい。
の大きさを求めなさい。
(2) 円すいの表面積を求めなさい。

(1)であるが,
![]()
を用いて,
![]()
(2)は, 側面積
![]()
を用いて,
![]()
この
![]()
40
 数樂管理人のブログ
数樂管理人のブログ 

