こんにちは。相城です。題の通り, 連立方程式を文字で置いて解いてみようということです。
連立方程式の一般解を求めよう
連立方程式の一般式
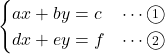
を解いてみましょう。
先ず,
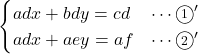
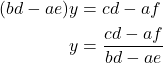
次にこの
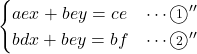
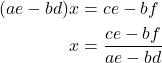
よって, この連立方程式の解は,
![]()
何か普通に終わってしまいましたね。これが連立方程式の一般解です。
しかし, ここでこの解の
![]()
これで解を書き直すと,
![]()
となり、解の2数の分母が同じであることが分かる。
こんにちは。相城です。題の通り, 連立方程式を文字で置いて解いてみようということです。
連立方程式の一般解を求めよう
連立方程式の一般式
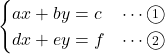
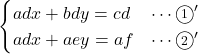
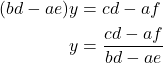
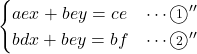
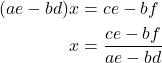
![]()
![]()
![]()