こんにちは。相城です。今回も少し違った角度から連立方程式を見ていきましょう。登場するのは直線束の考え方(気になる方は下段の関連記事からどうぞ)です。
一見面倒に見えるけど
連立方程式
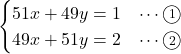
を解け。
このような連立方程式があった場合,
恐らく
それでできないことはありませんが, 計算が大変です。
ここでは, 連立方程式の特性(直線束の考え方)を活かした解法で行こうと思います。
この連立方程式の解を
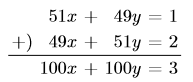
として, 新たに式を作った式![]() もまた,
もまた, ![]() を満たしている。
を満たしている。
同様に,
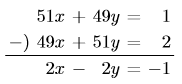
として得られる式![]() も,
も, ![]() を満たしている。
を満たしている。
このことは, 新たに
連立方程式
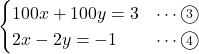
とした連立方程式を解いても, その解は
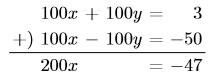
より, ![]()
そしてこれを代入するのではなく, 今度は引き算して, ![]() を求める。
を求める。
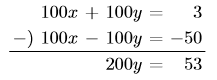
より, ![]()
よって, この連立方程式の解は,
![]()
となる。
よく私立高校の入試問題で見られます。そのまますると計算が大変ですが, 一工夫すると楽にできてしまいますね?
ではでは。
 高校数学:交点を通る直線(束)・GeoGebra付
高校数学:交点を通る直線(束)・GeoGebra付  中学数学:連立方程式の解法研究
中学数学:連立方程式の解法研究 数樂管理人のブログ
数樂管理人のブログ 
