こんにちは。相城です。今回は皆さん疑問に思ったことがあるかもしれません。連立方程式の増減の問題で, なんで今年の人数を![]() ,
, ![]() と置かないんだろうか?と。その疑問を見ていきましょう。
と置かないんだろうか?と。その疑問を見ていきましょう。
一般的な解法の裏側
問題:ある中学校で去年の生徒の人数は335人で, 今年は男子が5![]() 減り, 女子が4
減り, 女子が4![]() 増えたので全体としては1人減った。
増えたので全体としては1人減った。
今年の男子と女子の人数を求めなさい。
よくありきたりな中学2年生で習う連立方程式の割合(増減)の文章問題である。
通常去年の男子の人数![]() 人, 去年の女子の人数を
人, 去年の女子の人数を![]() 人として, 次のような連立方程式を立てるのが定石である。
人として, 次のような連立方程式を立てるのが定石である。
式1
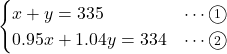
または,
式2
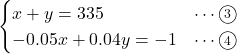
このどちらを解いても
答えを書くと、
今年の男子152人, 今年の女子182人
ここで, 式1の
形が違うだけで, まったく同じ式である。以下にそれを書いてみた。
![]()
展開して(かっこをはずして),
![]()
並べ替えると,
![]()
ここで, 下線部は式1の
従って次のようになる。
![]()
335を右辺へ移行して、整理すると,
![]()
となり, 式2の
式1の
式2の
今年の人数をx, yとしてみると
では, 最後に面倒な小数の計算して今年の人数を出すぐらいなら,
何で今年の男子の人数を![]() 人, 今年の女子の人数を
人, 今年の女子の人数を![]() 人としないのか, 納得いかない。
人としないのか, 納得いかない。
そういう方のために実際に今年の男子, 女子の人数をそれぞれ![]() 人,
人, ![]() 人としてやってみました。
人としてやってみました。
(解)今年の男子![]() 人, 今年の女子
人, 今年の女子![]() 人とおくと,
人とおくと,
![]()
去年の男子は![]() 人, 去年の女子は
人, 去年の女子は![]() 人
人
これより,
![]()
これより求める式は,
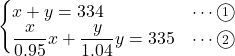
なんか面倒みたいですね。ただ答えが出ることを確認するために, 最後まで力ずくで行きましょう。
![]()
両辺に
![]()
![]()
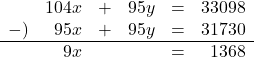
![]() , これを
, これを![]() に代入して,
に代入して, ![]()
よって,
今年の男子152人, 今年の女子182人![]() (答)
(答)
この解法で, ポイントは![]() の式でしょうね。結局式を作る過程で去年の人数を使うんだし, 今年の人数を
の式でしょうね。結局式を作る過程で去年の人数を使うんだし, 今年の人数を![]() ,
, ![]() とおくと, 去年の人数が分数になってしまう。それだったら去年の人数を
とおくと, 去年の人数が分数になってしまう。それだったら去年の人数を![]() ,
, ![]() とおいて, 今年の人数を求めた方が楽だってことでしょうね。
とおいて, 今年の人数を求めた方が楽だってことでしょうね。
今年の人数を![]() ,
, ![]() とおいて答えが出ないわけではないです。面倒なだけなのです。
とおいて答えが出ないわけではないです。面倒なだけなのです。
 数樂管理人のブログ
数樂管理人のブログ 

