こんにちは。相城です。今回はねじれの位置の発見法です。ねじれの位置って日常で見かける場面と言えば, 立体交差点みたいな道路とか線路ですかね。それではどうぞ。
ねじれの位置の発見方法の基本パターン
例:図の立方体で, BCとねじれの位置にある辺を全て求めなさい。
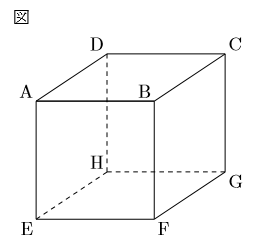
中1で必ず登場する問題である。
ねじれの位置とは, 同一平面上にない2直線の位置関係である。日常では立体交差点なんかが挙げられると思うのですが。
さて, ねじれの位置の発見方法はいたって簡単です。先の述べたように, 同一平面上にないのがねじれの位置なので, 同一平面上に あるものを消去していき, 残りをねじれの位置とします。以下手順です。例の文中は辺となっていますが, 以下直線と記してある場合があります。 ご了承を願います。
手順1:交わっている直線を消去
手順2:平行な直線を消去
手順1, 手順2で消去されず、残ったものがねじれの位置にある。
概ねこの手順で, ねじれの位置は発見できる。
では, 上の例を解いていきましょう。
手順1で交わっている直線を消去とあるが, 交わっているということは, ほとんどの場合, 対象となる直線のアルファベット1文字が含まれている。
例ではBCとねじれの位置にある~とあるので, BまたはCの文字が必ず1つ含まれる直線を消去する。(必ずそうとは限らないので注意。)
つまり, 手順1では, AB,DC,BF,CGが消去されます。
手順2では, BCに平行な直線が消去されます。つまり, AD,EH,FGが消去されます。 手順1, 2が終了したとき, 消去されていないのが, ねじれの位置にある直線です。 例の場合, 残ったのはAE,DH,EF,HGで, これらの辺がねじれの位置にあります。 よって, (答)辺AE,DH,EF,HG
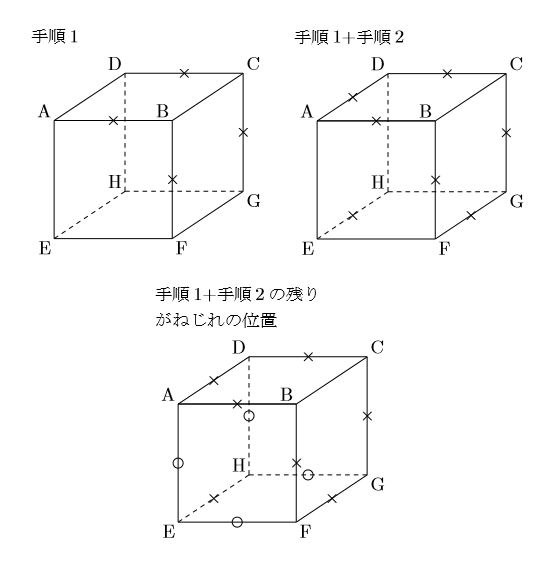
手順1で, 交わる場合でもアルファベットを含まない場合があります。例えば, 直方体を斜めに切断した立体などのねじれの位置を探す場合です。
下の図の場合, 例えば, 右の図の立体で, 辺BFとねじれの位置にある辺を全て求めなさい。と問題にあった場合, 手順1でBC,BA,FE,FGが消去され, 手順2でCGが消去される。残った辺がねじれの位置と言いたいところだが, ここで注意すべきはAEである。AEはBFを含む平面上にあるので, AEはBFとはねじれの位置にない。よって, ねじれの位置にある辺は, 辺HG,DC,DH,HE,DAになります。AEとBFは同一平面上にあります。AEとBFはねじれの位置ではありません。
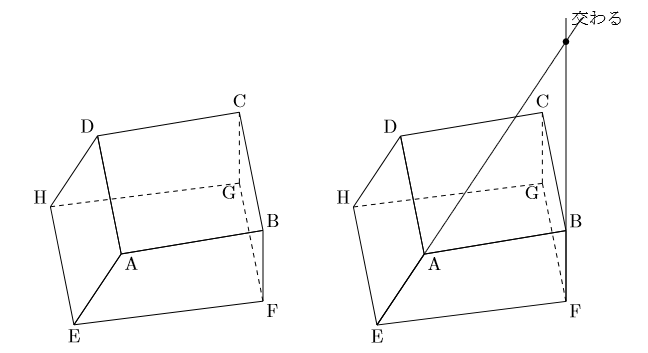
最後に, これを書いていてふと思ったのですが, ねじれの位置にある辺を探すのに, 先ず対象の辺を含む平面の辺を全て消去したほうが, 早いんじゃないでしょうか。 例えば, このページの例をとってみると, BFが対象なので, BFを含む面ABFE, CBFGの辺を全て消去し, 手順に入っていけばよいのかな, なんて思ってみました。そっちの方がいい気がします。ご参考にしてください。
同一平面上にある辺(平行・垂直・交わる)を削除し, 残りをねじれの位置とする
 数樂管理人のブログ
数樂管理人のブログ 

