中学数学：攻略・素因数分解

2020年4月12日2022年5月29日

SHARE

こんにちは。相城です。今回は素因数分解についてです。

素数と因数

先ず素数について。素数とは, 1とその数自身しか約数にもたない数のことです。例えば, 1は約数が1しかないので素数ではない, 2は約数が1, 2なので素数, 3は約数が1, 3なので素数, 4は約数が1, 2, 4なので素数ではない。 5は約数が1, 5なので素数, $\cdots$ 以下20までの中に素数は, 2, 3, 5, 7, 11, 13, 17, 19の8個あります。また, 素数は無限にあります。

次に因数というものがあります。因数とは約数のことです。

6の因数は1, 2, 3, 6になります。

この因数の中に素数の因数があります。2と3です。これを素因数といい, ある数を素因数で分解して積の形で表すことを, 素因数分解といいます。

したがって6を素因数分解(素数の積で表す)すると

$6=2\times3$

となります。
では12はどうでしょうか。12になる掛け算を $1\times12$ 以外で挙げてください。例えば, $2\times6$ ですね。

$12=2\times 6$

でも素数の積で表すことが目的なので, 素数でない6は, まだ分解しなくてはいけません。 6 $=2\times3$ と分解できるので,

$12=2\times2\times3$

同じ数の積は累乗を使わないといけないので,

$12=2^2\times3$

となって, 12を素因数分解(素数の積の形に)できました。

素因数分解の方法

ではいちいちこうやって掛け算に直すのか？というのがありますが, そんな面倒なことはしません。割り算の筆算を逆さまにした記号を使って, 筆算していきます。私は逆筆算とか適当に名前つけていますけどね。
こんな感じです。

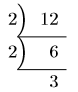
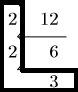
12の素因数分解の結果は黒の太線の中なので, 12の素因数分解の結果は

$2^2\times3$

となります。特に断りのない限り, 素数は小さい順に並べます。
もう一つ例題をどうぞ。
60の素因数分解は

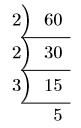
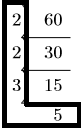
60の素因数分解の結果も黒の太線の中なので, 60の素因数分解の結果は

$2^2\times3\times5$

素数は小さい順に並べましょう。

素因数分解することで, その数の性質が分かるんですね。約数が何個あるとか, 何の倍数なのかなんかが。
ではでは。

プリントアウト用pdf

コメントを残すコメントをキャンセル

前の記事

中学数学：攻略・乗法公式と展開

次の記事

中学数学：攻略・平方根の値