中学数学：攻略・一次関数の式を求める

2020年4月13日2022年5月3日

SHARE

こんにちは。相城です。今回は一次関数の式を求めるコツをお伝えできればと思います。それではどうぞ。

注意すること

座標の表現方法として(1, 3)という座標を $x=1$ , $y=3$ と表すことがあります。これは同じ意味です。
また, 座標(1, 3)を” $x=1$ のとき $y=3$ となる”という言い方もありますが, 同じ意味です。

傾きと切片がわかる

(1) 傾きが $2$ で, 切片が $-3$ の直線の式を求めなさい。

直線の式は $y=ax+b$ と表され, $a$ は傾き(変化の割合)で, $b$ は切片なので,

$y=2x-3$

傾きと通る1点がわかる

(2) 変化の割合が3で, 点( $-1, 2$ )を通る直線の式

変化の割合が $-1$ なので, 求める直線の式を $y=-x+b$ と置く, これが( $-1, 2$ )を通るので, $2=-(-1)+b$ として, $b=1$ 。よって, 求める直線の式は

$y=-x+1$

切片と通る1点がわかる

(3) 切片が3で $x=-2$ のとき, $y=9$ となる直線の式を求めなさい。

求める直線の式を $y=ax+3$ と置いて, $x=-2$ , $y=9$ を代入すると, $9=-2a+3$ となり, $a=-3$ となる。よって, 求める直線の式は

$y=-3x+3$

通る2点がわかる

(4) 2点( $1, -2$ ), ( $5, 6$ )を通る直線の式を求めなさい。

解法１：変化の割合を求めると $\dfrac{6-(-2)}{5-1}=2$ となるので, 求める直線の式を $y=2x+b$ と置いて, 2点のどちらかを代入して $b$ を求めると, $b=-4$ 。よって, 求める直線の式は

$y=2x-4$

解法２：求める直線の式の形は $y=ax+b$ なので, 2点をこれに代入して, $a$ , $b$ の連立方程式をつくると,

$\begin{eqnarray*} \begin{cases}a + b = -2\\5a + b = 6\end{cases} \end{eqnarray*}$

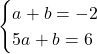
これを解いて, $a=2$ , $b=-4$
よって, 求める直線の式は

$y=2x-4$

個人的には解法2をお勧めしてます。理由は座標が分数のときも使いやすいから。

～に平行、～と平行

(5) 一次関数 $y=2x-5$ と平行で, 点(1, 3)を通る直線の式を求めなさい。

ここでの重要用語は～平行で, という言葉。これは求める直線の傾きは問題にある直線の傾きと同じになるということを意味している。
傾きが同じでなければ, グラフはいつか交わってしまいますから。

ですから, 求める直線の式は $y=2x+b$ とおくことができ, この直線が点(1, 3)を通ることから,

$3=2\times 1+b$

として, $b=1$ を得る。よって求める直線の式は

$y=2x+1$

x軸上と交わる

(6) 一次関数 $y=2x-4$ と $x$ 軸上で交わり, 点(1, 3)を通る直線の式を求めなさい。

ここでの重要用語は $\underline{\bf{x}}$ 軸で交わり, という言葉。これは $y=2x-4$ において $y=0$ とした場合, $x$ の値を求めると,

$0=2x-4$

より, $x=2$ となり, $x$ 軸との交点は $(2, 0)$ となる。求める直線は, (2, 0)と(1, 3)を通るので, その直線の式は

$y=-3x+6$

y軸上で交わる

(7) 一次関数 $y=3x+5$ と $y$ 軸上で交わり, 点(1, 3)を通る直線の式を求めなさい。

ここでの重要用語は $\underline{\textbf{y}}$ 軸上で交わり, という言葉。これは求める直線の式の切片が, $y=3x+5$ の切片と同じであるということを意味している。
したがって, 求める直線の式は, $y=ax+5$ とおくことができる。この直線の式が, 点(1, 3)を通るので,

$3=a \times 1+5$

として, $a=-2$ を得る。よって求める直線の式は

$y=-2x+5$

xの増加量・yの増加量

(8) その他, $x$ の値が3増加するとき, $y$ の値は6減少し, 点(1, 3)を通る直線の式を求めなさい。

を用いれば, 傾き $=\dfrac{-6}{3}=-2$ と出せるので, 求める直線の式を $y=-2x+b$ と置いて, (1, 3)を代入すると, $3=-2\times1+b$ , $b=5$ となるので, 求める直線の式は

$y=-2x+5$

一次関数の式を求めることは, 中学2年生で学ぶ重要な内容の1つですので, しっかりマスターしてください。

プリントアウト用pdf

コメントを残すコメントをキャンセル

前の記事

中学数学：演習問題・素因数分解②

次の記事

中学数学：正負の数⑦2数の乗法