こんにちは。相城です。今回は3辺の長さが既知の三角形の面積を求めてみたいと思います。必ず求まりますので根気よく行きましょう。それではどうぞ。
三角形の面積を求めるにあたって, 三角形の3辺の長さが分かっていれば, 面積は必ず求められるという事実を ご紹介いたしましょう。まず, 三角形の高さが三角形の内部にできる場合を考えます。下の図で, 3辺の長さは, 7, 5, 3である。 長さ7の部分が底辺になっていると考えてください。 そのときの高さをADとします。次にDCを![]() とおきます。するとBD
とおきます。するとBD![]() となります。
となります。
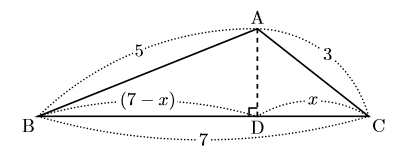
ここで, 線分ADは△ABDと△ACDに共通な辺であり, それぞれの三角形に三平方の定理を用いると,
![]()
![]()
となり,
![]()
となる。これを解いて
![]()
次に高さが三角形の外部にできる場合を考えても同様のことがいえることを表してみる。三角形の3辺の長さ, 頂点は, 先と同じにしている。 このとき, 底辺はCAで, 高さは点Bから直線CAに下ろした垂線で, 線分BDである。
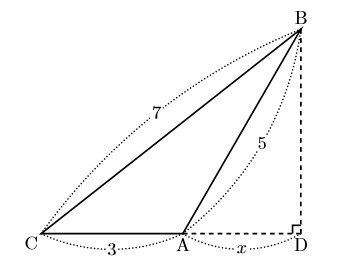
このとき, AD=![]() とすると, CD
とすると, CD![]() となる。高さBDは△BCDと△BADに共通であるから, それぞれに三平方の定理を用いると,
となる。高さBDは△BCDと△BADに共通であるから, それぞれに三平方の定理を用いると,
![]()
![]()
となり,
![]()
となる。これを解いて
求める面積は,
![]()
と当たり前だが, 先の答えと同じになる。
このように3辺の長さが分かっていれば, 必ず三角形の面積が求まることを知っておきましょう。ちょっとした応用問題に使える知識ですので,
数学で得点アップを目指すのであれば, 覚えておきたい知識と技ですね。ではでは。
ちなみに3辺の長さが分かっている場合の公式として有名なのがヘロンの公式というのがある。興味がある方はぜひ調べてみましょう。
 数樂管理人のブログ
数樂管理人のブログ 

