中学数学：攻略・速さの文章問題

こんにちは。相城です。今回は速さの問題の攻略方法です。これを機に速さの文章問題や文字式が得意になればと思います。それではどうぞ。

基本公式を覚えておこう

皆さんご存知かと思いますが, キハジ(距離・速さ・時間), ミハジ(道のり・速さ・時間)の覚えるための図を右に書いてみました。皆さんご存じでしょうかね？ (ちなみにオームの法則や比例反比例もこの図に当てはめて覚えることが可能です。)
まぁもっともこの図を書ける人は多いのですが,
使えるようになるにはなかなか難しいものがありますかね？ただ道のりを求めるときは掛け算, それ以外は割り算と思っておけば少しは楽かもしれません。僕なりにアレンジしてみました。

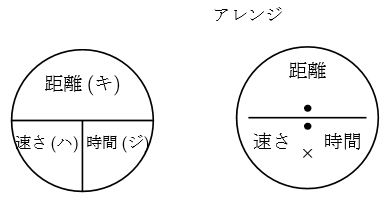
今回は, これが書けても式が作れないという方へのメッセージです。こんな方法もあったんだということを知っていただいて, 問題攻略に役立ててくださればと思います。

では, どう使うか例題を見て, 使い方を見ていきましょう。

例題1

【例題1】地点Aと地点Cは13\,km離れています。太郎君は, 地点Aから地点Bまでは時速4kmで歩き, 地点Bから地点Cまでは時速5kmで歩いたとき, 合計で3時間かかりました。
地点Aから地点Bまでを $x$ km, 地点Bから地点Cまでを $y$ kmとして, $x$ , $y$ の値を求めなさい。

解法のテクニック

こんな時, 上のキハジの〇が書けるのなら距離(キ) $=x$ km, そのときの速さ(ハ) $=$ 時速4kmとして, 上の○のキ, ハに書き込みます。すると左下のように時間(ジ) $=\dfrac{x}{4}$ 時間が求まります。同様に, 距離(キ) $=y$ km, そのときの速さ(ハ) $=$ 時速5kmとして, ○のキ, ハに書き込みます。すると, 右下のように時間(ジ) $=\dfrac{y}{5}$ 時間が求まります。

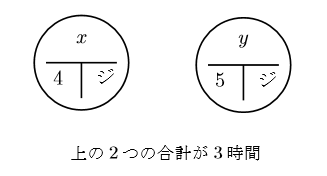
この2つの合計が3時間なので,
$\dfrac{x}{4}+\dfrac{y}{5}=3$
と式ができます。
もっとも
$x+y=13$
はできるという前提にはなりますが。これで少し, 式の作り方が見えてきましたかね。では, 続きをいってみましょう。

例題2

【例題2】地点Aと地点Cは1800m離れています。太郎君は, 地点Aから地点Bまでは分速40mで歩き, 地点Bから地点Cまでは分速60mで歩いたとき, 合計で35分かかりました。
地点Aから地点Bまでを $x$ 分, 地点Bから地点Cまでを $y$ 分として, $x$ , $y$ の値を求めなさい。

解法のテクニック

こんな時, 上のキハジの〇が書けるのなら速さ(ハ) $=$ 分速40m, 時間(ジ) $=x$ 分として, 上の○のハ, ジに書き込みます。すると, 左下のように距離(キ) $=40x$ mが求まります。同様に, 速さ(ハ) $=$ 分速60m, 時間(ジ) $=y$ 分として, ○のハ, ジに書き込みます。すると, 右下のように距離(キ) $=60y$ mが求まります。