中学数学：勝利の方程式・勝ちパターンに持ち込む

こんにちは。相城です。数学の問題に取り組むときの心構えのようなものをお伝えできればと思います。

勝利の方程式を使う

私が今まで指導してきて思うのは, 数学を苦手とする人は, 勝利の方程式を使えていないことが多いことに気付かされます。
ここでいう勝利の方程式とは, 各個人違うものでありますが, 基本的な考え方は同じです。以下に例を示しながら, どういったことを意識していけば, 少しでも問題が解けるようになるかということを書きたいと思います。読み終わって, そういうことか。
じゃ私もやってみようとなってくだされば, 幸いに存じます。

さて, 例えば以下の連立方程式が加減法なら解ける生徒がいたとします。(実際加減法で解く生徒が多いのですが。)

$\begin{eqnarray*} \begin{cases}2x + 5y = 26\\x + y = 10\end{cases} \end{eqnarray*}$

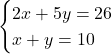
しかし, 上の連立方程式が, 次のようになったとたんに解けなくなります。

$\begin{eqnarray*} \begin{cases}5y = 26-2x\\x + y = 10\end{cases} \end{eqnarray*}$

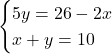
もう何が何だかわけわからないということなのでしょうけれども。

ここで初めの連立方程式が加減法で解けるのなら, 次に出てきた連立方程式も加減法で解くように仕向ければよいのです。
これが, 私のいう勝利の方程式です。
つまり, $5y=26-2x$ を $2x+5y=26$ という加減法で解く形に持っていくということです。
自分が苦手なものは, 自分が得意とする方法で解けばよいのです。勝ちパターンに持ち込んでいくのです。もし仮に代入法の形で出題されても解き方に指示がなければ, 加減法で解いても何ら問題ありません。
実際入試には加減法で解きなさい, 代入法で解きなさいなんて指示は出ませんから。

次に同じような例を示します。

2次方程式 $x^2-3x+1=0$ を解きなさい。これが解の公式を使って解けるのに, $x^2-3x=-1$ となると解けない。これも同じ理屈で,
解の公式で解ける形に持ち込むのが, 勝利の方程式です。もちろん $(x+3)^2=5$ となっている式もこの形で解けないのなら,
左辺を計算して( $=$ の左側のかっこをはずして), 右辺( $=$ の右側)を左辺に持ってきます。そして, いつものように解の公式で解けばよいのです。
もちろん因数分解ができない場合も同じです。計算にかかる時間は少し長くなりますが, 正解を得るための手段を確かなものにするためには,
それぐらいのリスクは大きくないと思います。

数学が得意な人からするとなんて非効率な, そんなんじゃだめだと仰ると思いますが, 数学が苦手ない人からすると,
できるだけ作業化して, 少しでも解けることを実感していただいた方が, よいと思います。ただ, このように伝えても数学が苦手な人は,
なかなか覚えることができません。それぐらい数学が遠い存在なのです。

ここに記したのが, 主ではありますが, 勝利の方程式はあなたの中にあります。
その勝利の方程式を使って,少しでも問題を解いていきましょう。

数学が苦手な人は, 数学って意外と簡単じゃん。なんだこんなことでできるんだ。って興味を持っていただきたいです。
そして少しでもあきらめずに解いて, 徐々に数学を好きになってくださいね。

攻略のポイント

勝利の方程式・勝ちパターンを作って, それに持ち込む。

プリントアウト用pdf

【GOM Mix】初心者でも簡単な動画編集ソフト