中学数学：攻略・角度の頻出テクニック1(証明)

こんにちは。相城です。さて, 三角形の合同の証明で頻出の角の表記方法について触れたいと思います。おそらくもうすでに見た方がいるかもしれません。中2・中3生は是非。それではどうぞ。

証明における頻出テクニック

証明問題で頻出の角の表記方法を書いてみました。黄色の枠内の部分はぜひ使いこなせるようにしておきたいですね。

【EX】右の図で, 四角形ABCDは長方形で, 線分PQを折り目として長方形を折り返すと, 点Aが点Cと重なった。このとき, △PBC $\equiv$ △QRCを証明しなさい。

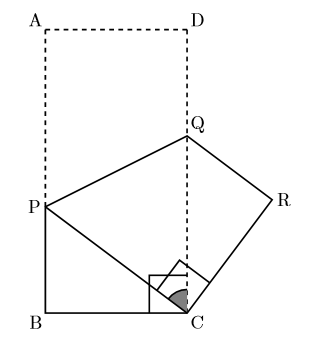
よく使う技
同じ大きさの角から共通部分を引く。
この場合, $90^{\circ}(\angle{\text{PCR}}, \angle{\text{QCB}})$ が同じ大きさで, 共通部分が $\angle{\text{QCP}}$ となり,

この表記テクニック

$\angle{\text{PCB}}=90^{\circ}-\angle{\text{QCP}}$
$\angle{\text{QCR}}=90^{\circ}-\angle{\text{QCP}}$
これより, $\angle{\text{PCB}}=\angle{\text{QCR}}$

【EX】右の図で, 四角形ABCDは平行四辺形であり, 辺BC, 辺CDを1辺とする正三角形を図のように作ります。点A, Fと点A, Eを結ぶ。またAEとBC, AFとDCの交点をそれぞれG, Hとする。このとき, △ABE $\equiv$ △FDAであることを証明しなさい。

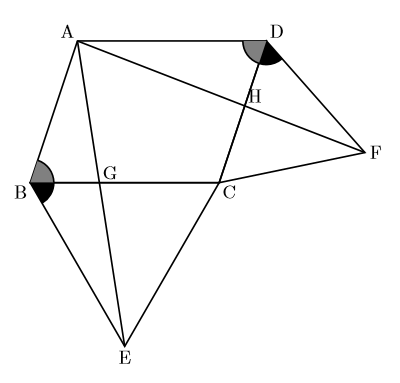
よく使う技
同じ大きさの角に同じ大きさの角を足す。
この場合, $60^{\circ}$ (黒色 $\angle{\text{EBC}}, \angle{\text{FDC}}$ ),
灰色( $\angle{\text{ABC}}, \angle{\text{CDA}}$ )が同じ大きさで,

この表記テクニック

$\angle{\text{ABE}}=60^{\circ}+\angle{\text{ABC}}$
$\angle{\text{FDA}}=60^{\circ}+\angle{\text{CDA}}$
$\angle{\text{ABC}}=\angle{\text{CDA}}$ であるから,
$\angle{\text{ABE}}=\angle{\text{FDA}}$

この角度の表記テクニックはぜひマスターしておくべきでしょう。中学を卒業までに必ずと言っていいほど出題されます？(言いすぎかな・・・)
このテクニックは合同の証明だけでなく, 中3で出題される相似の証明にも使えますからぜひ習得してください。

プリントアウト用pdf

証明における頻出テクニック

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル