中学数学：攻略・角度の頻出テクニック2(証明)

こんにちは。相城です。証明でよく使うテクニックの第2弾。前回とよく似ていますが, 図形が少し違うので出しておきます。直角三角形と正三角形で, ともに単体の場合です。それではどうぞ。

証明における頻出テクニック1

証明問題で頻出の角の表記方法を書いた。※部分はぜひ使いこなせるようにしておきたい。

【EX】直角三角形ABCの頂点Cから辺ABに垂線を下ろし, 辺ABとの交点をDとする。このとき, △ACD∽△CDBを証明しなさい。

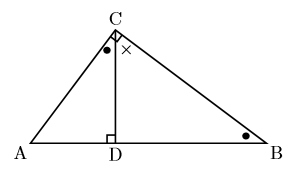
よく使う技
$\bullet+\times=90^{\circ}$ を使って, $\angle{\text{ACD}}=\angle{\text{CBD}}$ をいう。

この表記テクニック

$\angle{\text{ACD}}+\angle{\text{DCB}}=90^{\circ}$
$\angle{\text{CBD}}+\angle{\text{DCB}}=90^{\circ}$
これより,
$\angle{\text{ACD}}=\angle{\text{CBD}}$

証明における頻出テクニック2

【EX】右の図のように, 一辺が6cmの正三角形があります。辺BCを2 : 1に分ける点をDとして, $\angle{\text{ADE}}=60^{\circ}$ となる点Eを辺AB上にとる。このとき, △ACD∽△DBEであることを証明しなさい。

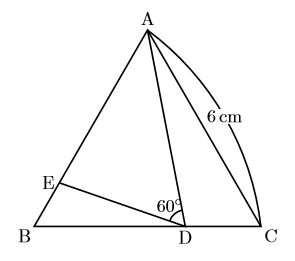
よく使う技(三角形の外角の定理:三角形の外角は, それととなりあわない2つの内角の和に等しい。)

この表記テクニック

$\angle{\text{DAC}}+60^{\circ}=\angle{\text{EDB}}+60^{\circ}$
よって,
$\angle{\text{DAC}}=\angle{\text{EDB}}$
ちなみに上の式で左辺の $60^{\circ}$ は $\angle{\text{ACB}}$ のことである。

終わりに

これらの角度の表記テクニックはぜひマスターしておくべきでしょう。
このテクニックは, 中3で出題される相似の証明によく出題されますので覚えておいてください。
これらは中2生もしっかり覚えておくといいでしょう。特に初めの直角三角形は直角三角形の合同で見られることもあります。
皆さん, しっかり習得してくださいね。

プリントアウト用pdf

証明における頻出テクニック1

証明における頻出テクニック2

終わりに

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル