こんにちは。相城です。今回は列車の文章問題を見ていきましょう。いきなり余談ですが, なぜ列車なのかは, 私の住んでる徳島県に電車がないから, 電車じゃなく列車にしているといううわさがありますが, 真意は存じません。それではどうぞ。
ある列車が, 長さ680mの鉄橋を渡り始めてから渡り終わるまでに40秒かかった。また, 同じ列車が長さ1020mのトンネルにすっかり隠れているのが45秒であった。 列車の長さと速さはともに同じとして, 速さは常に一定とするとき, 列車の長さと速さを求めなさい。
速さの問題では, 基本公式
(道のり)=(速さ)![]() (時間)
(時間)![]()
が基本になります。
列車が680mのトンネルを渡り始めてから渡り終わるまでをイラストにすると以下のようになります。 ただし, 列車の長さは![]() m, 列車の速さは
m, 列車の速さは![]() m/秒とします。
m/秒とします。
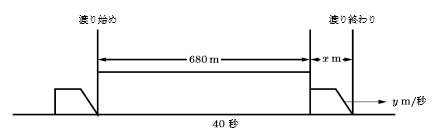
このイラストからわかるように, 列車は鉄橋を渡り始めてから, 渡り終わるまでに, 単に680m走るのではなく, 列車の長さ分を加えた長さ 680+![]() (m)を走っていることが分かります。このときかかった時間が40秒で, 列車の速さが
(m)を走っていることが分かります。このときかかった時間が40秒で, 列車の速さが![]() m/秒でありますから, 速さの公式①から
m/秒でありますから, 速さの公式①から
![]()
次に列車が, 長さ1020mのトンネルにすっかり隠れている時間が45秒であったというのをイラストにしてみると,
以下のようになります。
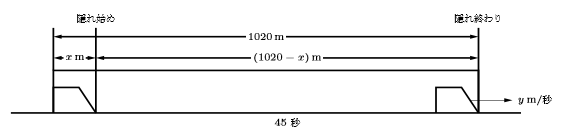
列車はトンネルに隠れ入ってから, トンネルを隠れ出る瞬間までは, トンネルの長さから列車の長さを引いた距離を 走っていることが分かります。このときかかった時間が45秒で, 列車の速さが![]() m/秒でありますから,
m/秒でありますから, ![]() 求めたときと同様の
求めたときと同様の
考え方で,
![]()
よって,
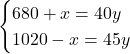
これを解いて,
よって, 列車の長さ120m, 列車の速さ20m/秒
となります。
このような感じで式をつくっていけば解くことができるようになります。
 数樂管理人のブログ
数樂管理人のブログ 

