こんにちは。相城です。証明での角度の記述で頻出テクニックを紹介しておりますが, 今のところこれが最後になります。それではどうぞ。
相似系の問題でよくあるのが, この問題である。
【EX】
右の図のような, ![]() の台形があります。 辺BC上に点Pを,
の台形があります。 辺BC上に点Pを, ![]() となるようにとるとき, △ABP∽△PCDを証明しなさい。
となるようにとるとき, △ABP∽△PCDを証明しなさい。
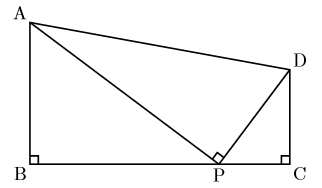
よく使う技

![]() を使って,
を使って, ![]() をいう。
をいう。
この表記テクニック①
![]()
![]()
これより,![]()
これでも十分いいのですが, 少し目線を変えると, もう少しすっきりする。 それは三角形の外角の定理を用いることである。
【定理】三角形の1つの外角はそれととなりあわない2つの内角の和に等しい。
というものである。△ABPに着目すると, その外角![]() は
は![]()
となる。これを用いると,
この表記テクニック②
![]()
これより,![]()
となる。こっちのほうがすっきりする。
上の問題では3つの角(![]() )が
)が![]() であるが, 上記の表記テクニック②のパターンの代表的なもをご紹介する。それは, 3つの角が
であるが, 上記の表記テクニック②のパターンの代表的なもをご紹介する。それは, 3つの角が![]() (正三角形)と
(正三角形)と![]() (直角二等辺三角形)の場合である。 その図を以下に書いておく。解法のご参考までに。
(直角二等辺三角形)の場合である。 その図を以下に書いておく。解法のご参考までに。
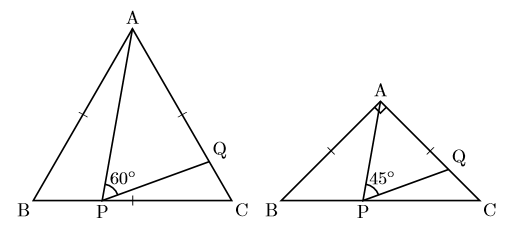
表記テクニック②の使用例
![]()
これより,![]()
![]() を
を![]() に変えれば直角二等辺三角形でも可なのはわかっていただけると思う。
に変えれば直角二等辺三角形でも可なのはわかっていただけると思う。
 数樂管理人のブログ
数樂管理人のブログ 

