中学数学：攻略・セパレイト計算方式

こんにちは。相城です。デカルトの困難は分割せよ。みたいな発想で生まれた計算方法です。正攻法のやり方ではないかもしれませんが, もし単項式の乗除で特に分数の計算が苦手な方がいたらご参考にしてください。

セパレイト計算方式

みなさんは中学2年生で, 次のような計算を習いました。またこれから習う人もいるでしょう。
次のような計算式です。
$3a^2\times ab^2=3a^3b^2$
$24x^2y\div 8xy=3x$
このような単項式の乗除の計算です。さて, この計算で重要な学びとは文字の逆数だと考えます。2の逆数が $\dfrac{1}{2}$ であるように, $x$ の逆数は $\dfrac{1}{x}$ を学ぶところでもあります。そして, 慣れてくれば， $\dfrac{2}{3}ab$ の逆数は $\dfrac{3}{2ab}$ と分かってくるのです。
ですから,次の計算はこのようにできます。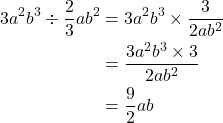
$\begin{aligned}3a^2b^3\div\dfrac{2}{3}ab^2&=3a^2b^3\times\dfrac{3}{2ab^2}\\&=\dfrac{3a^2b^3\times 3}{2ab^2}\\&=\dfrac{9}{2}ab\end{aligned}$
この計算がスラスラできる人は, 複雑な文字をかけ合わせたり, 割ったりできているに違いありません。
ただ, これの苦手とする所以は, 逆数にできない。逆数にしても式が複雑になり, 何が消去されて, 何が残っているのか判断がつかなかったり, 様々です。今回紹介する方法は, 逆数にできなくても？計算を楽にする方法をご提案します。これで完璧というわけではありません。どうしてもという方には, これを試してみてください。案外使えたりします。名付けてセパレイト計算方式です。今考えついた呼び名ですので, 申し訳ありませんが。以下にその方法を例題をもとに書きます。
通常の方法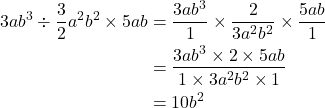
$\begin{aligned}3ab^3\div\dfrac{3}{2}a^2b^2\times 5ab&=\dfrac{3ab^3}{1}\times\dfrac{2}{3a^2b^2}\times\dfrac{5ab}{1}\\&=\dfrac{3ab^3 \times 2 \times 5ab}{1 \times 3a^2b^2 \times 1}\\&=10b^2\end{aligned}$
セパレイト計算方式
$3ab^3\div\dfrac{3}{2}a^2b^2\times{5ab}$
係数と文字に分離
係数のみ計算
$3\div\dfrac{3}{2}\times 5=10\cdots$ (係数決定 $\maru1$ )
文字の部分のみ計算
$ab^3\div a^2b^2 \times ab=b^2\cdots$ (文字決定 $\maru2$ )
そして,係数と文字を掛ける
$\maru1\times\maru2=10b^2$
この方法は, ここで学ぶことを逸脱しているかもしれないが, セパレイト方式では文字の逆数を扱わなくて済むことが多く, 比較的解きやすい解法かと考えます。もしよろしければ, 実践してみてください。
面白いですよ。