中学数学：攻略・ブーメランを使いこなせ

こんにちは。相城です。ブーメランを使いこなすと結構便利です。それではどうぞ。

ブーメランって何？

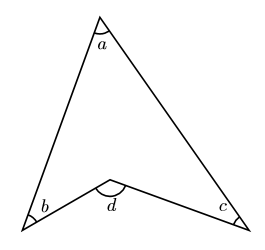
右の公式を習ったことを覚えているだろうか。僕はこれをブーメランと呼んでいます。
このブーメランでは次の公式が成り立つ。

$\angle{d}=\angle{a}+\angle{b}+\angle{c}$

このブーメランは結構活躍すると思うのだが, 実際の入試ではあまり見かけない。定期テストとかで, でてきたとき, たまたま入試で出題されたときなんかにご利用ください。

どんなときに使うか

どんなときに使うのか。例を3つほど書きました。
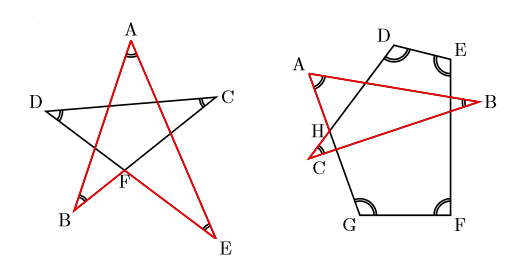
下の左の星形の印を付けた5つの角の和は180 $^{\circ}$ であることはご存知でしょう。赤のブーメランの3つの角の和は $\angle{\text{DFC}}$ と一致します。つまり印を付けた角の和は $\angle{\text{DFC}}$ の内角の和と一致するのです。

もう一つはその右の図。同じような7つの印を付けた角の和を求めるとき, 赤のブーメランの角の和は $\angle{\text{DHG}}$ と一致します。
つまり, 印を付けた7つの角の和は五角形DHGFEの内角の和と一致します。よって, 印を付けた7つの角の和は540 $^{\circ}$ となります。

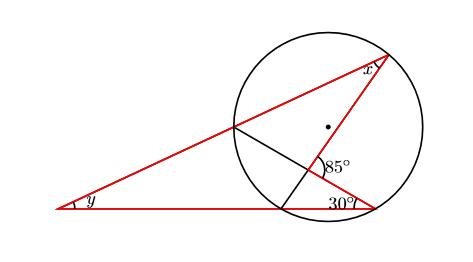
中3で出てくる円周角の問題でも使えちゃいます。下の $\angle{x}$ は円周角の定理より30 $^{\circ}$ 。赤のブーメランは公式より $\angle{y}=85^{\circ}-30^{\circ}\times2=25^{\circ}$ となります。

このように結構使えるので, このブーメラン公式は覚えておきましょう。

これにも使える

ブーメランの公式を用いると,中2で習う下の図で $\angle{x}$ を求める問題で,
$\angle{x}=\angle{a}+(\bullet+\times)$
$\angle{a}=\angle{x}-(\bullet+\times)$
が成り立ちます。

実際下の問題では,
$2\bullet+2\times=140^{\circ}$
両辺2で割って,
$\bullet+\times=70^{\circ}$

よって,
$\angle{x}=40^{\circ}+70^{\circ}=110^{\circ}$
となります。

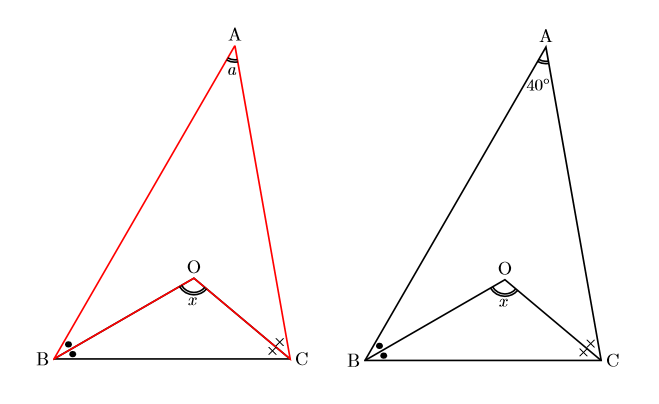
△OBCから $\bullet$ と $\times$ を引いて $\angle{x}$ を求めるという考え方でも
$\angle{x}=180^{\circ}-(\bullet+\times)=180^{\circ}-70^{\circ}=110^{\circ}$
と答えは一致します。

また別の公式
$\angle{x}=90^{\circ}+\dfrac{\angle{a}}{2}$
と照らし合わせると,
$\angle{a}+(\bullet+\times)=90^{\circ}+\dfrac{\angle{a}}{2}$
より,
$\bullet+\times=90^{\circ}-\dfrac{\angle{a}}{2}$
となりますが, これは単純に△ABCの内角の和
( $\angle{a}+2\bullet+2\times=180^{\circ}$ )から導けるものです。