こんにちは。今回は高知県の問題からです。
下の図において, ![]() は関数
は関数![]() のグラフで,
のグラフで, ![]() は傾き
は傾き![]() の直線である。
の直線である。![]() と
と![]() は点Aで交わり, 点Aの
は点Aで交わり, 点Aの![]() 座標は1である。また,
座標は1である。また, ![]() と
と![]() 軸の交点をBとする。このとき, 次の問1・問2に答えなさい。
軸の交点をBとする。このとき, 次の問1・問2に答えなさい。
(1) 点Bの座標を求めなさい。
(2) ![]() 軸上に
軸上に![]() 座標が正である点Pをとり, 点Pを通り
座標が正である点Pをとり, 点Pを通り![]() 軸に平行な直線が
軸に平行な直線が![]() ,
, ![]() と交わる点をそれぞれQ, Rとするとき, 次の(1)~(3)の問いに答えよ。
と交わる点をそれぞれQ, Rとするとき, 次の(1)~(3)の問いに答えよ。
① 点Pの![]() 座標が2のとき, 三角形AQRの面積を求めよ。
座標が2のとき, 三角形AQRの面積を求めよ。
② 三角形AQRの面積が27になる点Pの![]() 座標を求めよ。
座標を求めよ。
③ 三角形AQRの面積と三角形BPRの面積が等しくなるとき, 点Pの![]() 座標を求めよ。
座標を求めよ。
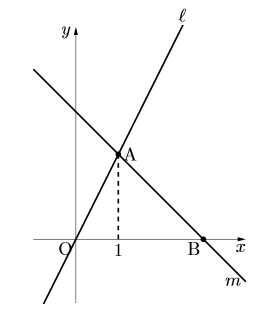
(高知県改)
 数樂管理人のブログ
数樂管理人のブログ 


最後の問題、三角形QOP=三角形AOBを使って解くと早いと思います!
ありがとうございます。
解答に追加しておきました。