数樂管理人のブログ 
こんにちは。今回は福岡県の入試問題からの出題です。
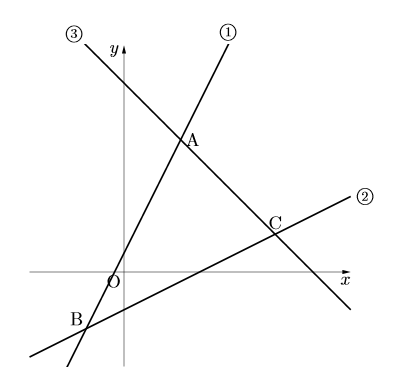
右の図で, 直線①, 直線②, 直線③の式は, それぞれ
, 
, 
ある。点Aは直線①と直線③の交点で, 点Aの座標は( 3, 7 )である。点Bは, 直線①と直線② の交点である。点Cは,
直線②と直線③の交点である。
次の(1), (2)は最も簡単な数で, (3)は指示にしたがって答えよ。
(1) 直線②と
軸の交点をDとし, 線分ODの中点をEとする。
軸上に点FをAF
FEの長さが最も短くなるようにとるとき, 点Fの座標を求めよ。
(2) 軸上の
に対応する部分に点Gを, △ABCの面積と△GBCの面積が等しくなるようにとるとき, 点Gの座標を求めよ。
(3) 点Bから直線③に垂線をひき, 直線③との交点をHとする。AH
CHとなるとき, 点Cの座標を
とし, 方程式をつくって点Cの座標を求めよ。解答は, 解く手順にしたがって書くこと。
(福岡県)
垂直な線が底辺を二等分しているので、三角形ABCは二等辺三角形。したがって、BA＝BCを示せれば良い。仮に、Aからy軸に垂直な線とBからx軸に垂直な線との交点をDとし、Bからy軸に垂直な線とCからx軸に垂直な線との交点をEとする。つまり、三角形ABDと三角形CBEが合同になれば良い。AとBと関係は、Bの座標から上方向に10進み、右に5進む。なので、Cの座標がBの位置から右に10進み、上方向に5進んだ場所にあれば良い。したがって、B（-2,-3)から右に10進み、上に5進んだ座標は、C（8,2)となる。これが一番綺麗だと思います。
いつもお世話になっています。
ありがとうございます。