こんにちは。相城です。まずは応用問題の入り口的な問題をやっていきましょう。
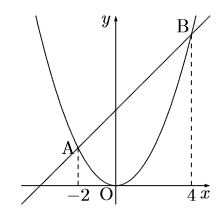
次のグラフは![]() と
と![]() のグラフです。この2つのグラフの交点をA, Bとし, その
のグラフです。この2つのグラフの交点をA, Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) ![]() で
で![]() の変域が
の変域が![]() のとき
のとき![]() の変域を求めなさい。
の変域を求めなさい。
(3) ![]() で
で![]() の値が
の値が![]() から
から![]() まで増加するときの変化の割合を求めなさい。
まで増加するときの変化の割合を求めなさい。
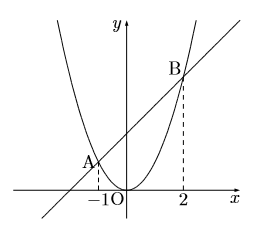
次のグラフは![]() と
と![]() のグラフです。この2つのグラフの交点をA, Bとし, その
のグラフです。この2つのグラフの交点をA, Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) ![]() で
で![]() の変域が
の変域が![]() のとき
のとき![]() の変域を求めなさい。
の変域を求めなさい。
(3) ![]() で
で![]() の値が
の値が![]() から
から![]() まで増加するときの変化の割合を求めなさい。
まで増加するときの変化の割合を求めなさい。
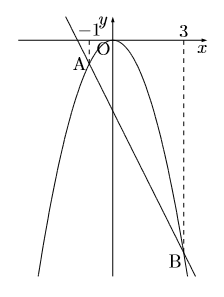
次のグラフは![]() と
と![]() のグラフです。この2つのグラフの交点をA, Bとし, その
のグラフです。この2つのグラフの交点をA, Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) ![]() で
で![]() の変域が
の変域が![]() のとき
のとき![]() の変域を求めなさい。
の変域を求めなさい。
(3) ![]() で
で![]() の値が
の値が![]() から
から![]() まで増加するときの変化の割合を求めなさい。
まで増加するときの変化の割合を求めなさい。
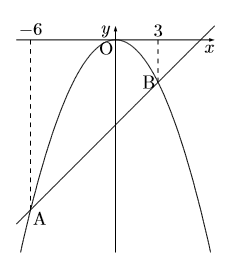
次のグラフは![]() と
と![]() のグラフです。この2つのグラフの交点をA, Bとし, その
のグラフです。この2つのグラフの交点をA, Bとし, その![]() 座標はそれぞれ
座標はそれぞれ![]() である。このとき次の問いに答えなさい。
である。このとき次の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) ![]() で
で![]() の変域が
の変域が![]() のとき
のとき![]() の変域を求めなさい。
の変域を求めなさい。
(3) ![]() で
で![]() の値が
の値が![]() から
から![]() まで増加するときの変化の割合を求めなさい。
まで増加するときの変化の割合を求めなさい。
 数樂管理人のブログ
数樂管理人のブログ 

