こんにちは。放物線の応用の基本的な問題です。それではどうぞ。
![]() のグラフがあり, Aの座標が(
のグラフがあり, Aの座標が(![]() ), また, ABは
), また, ABは![]() 軸に平行で,
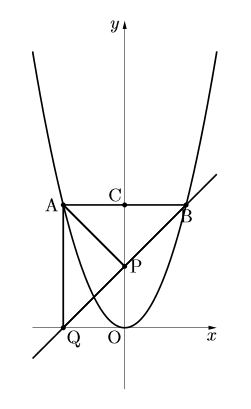
軸に平行で, ![]() 軸との交点をCとする。△APBが直角二等辺三角形になるように
軸との交点をCとする。△APBが直角二等辺三角形になるように![]() 軸上に点Pをとる。直線PBと
軸上に点Pをとる。直線PBと![]() 軸との交点をQとするとき, 次の問いに答えなさい。ただし, Pの
軸との交点をQとするとき, 次の問いに答えなさい。ただし, Pの![]() 座標は4より小さいものとします。
座標は4より小さいものとします。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) Pの![]() 座標を求めなさい。
座標を求めなさい。
(3) 直線PBの式を求めなさい。
(4) △ABQと△PBCの面積比を求めなさい。
(5) 点Cを通り△AQBの面積を二等分する直線の式を求めなさい。
 数樂管理人のブログ
数樂管理人のブログ 

