数樂管理人のブログ 
こんにちは。中1と言っておきながら中2以上のレベルかもしれません。中1の方はお気を付けください。それではどうぞ。
黒色と白色のタイルを, 黒, 白, 白の順をくり返し, 重ならないように左から右に並べていきます。
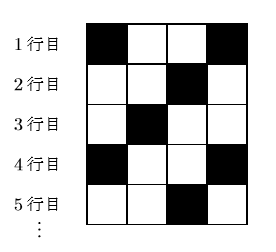
ただし, 図のように, 1行に4枚のタイルが並んだら, 次の行に, 前の行の4枚目に続く色のタイルを左から順に並べていきます。
この並べ方を続けるとき, 次の(1), (2)の問いに答えなさい。
(1) 1行目から9行目までタイルを並べるとき, 必要となる黒色のタイルの枚数を求めなさい。
(2) 
行目は, 左から3枚目が黒色のタイルとなります。1行目から行目までタイルを並べるとき, 必要となる黒色のタイルの枚数をを用いて表しなさい。
(宮城県)
多分中1の問題です。
簡単でした‼
面白かったです
だーれださん。
ありがとうございます。それはよかったです。
すいません何でKを置かずにいきなりn出しちゃダメなんですか
別解におかない方法を書きました。
ご覧ください。
すいません何でKを置いてnを後から代入しないといけないのですか
n行目というのが厄介なんだ。
n行目というのは2行目, 5行目, 8行目・・・ですよね。
黒のタイルは3, 7, 11, ・・・となる。k番目では4k-1
でもこのkというのは, 2行目, 5行目, 8行目・・・ではない。
だから, この2行目, 5行目, 8行目・・・をnとしてこの数をkを用いて表す。
すると, n=3k-1となって, これをkについて解くと, k=(n+1)/3となるってわけです。
そしてこれを4k-1に代入して答えを得るわけです。
先ほど回答に別解としてそれとは別の解法を載せましたのでご覧ください。
キャッシュがクリアになっていないと見れないかもしれませんが,
よろしくお願いします。
本当にありがとうございます
返信していただいて誠にありがとうございます