こんにちは。今回は大阪府のC問題を取り上げてみます。いい問題ですので取り組んでみてください。それではどうぞ。
![]() ,
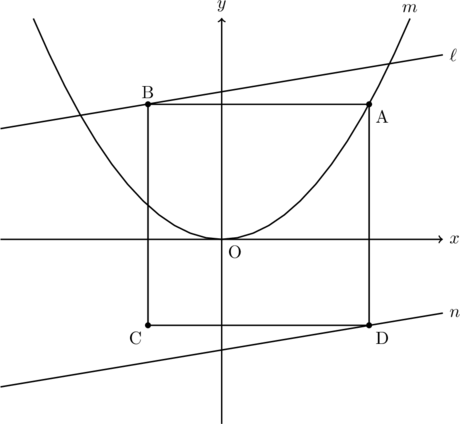
, ![]() を正の定数とする。下の図において,
を正の定数とする。下の図において, ![]() は関数
は関数![]() のグラフを表し,
のグラフを表し, ![]() は関数
は関数![]() のグラフを表す。
のグラフを表す。![]() は
は![]() と平行な直線であり, その切片は
と平行な直線であり, その切片は![]() である。四角形ABCDは正方形であり, ABは
である。四角形ABCDは正方形であり, ABは![]() 軸に平行であって, 辺ADは
軸に平行であって, 辺ADは![]() 軸に平行である。Aは
軸に平行である。Aは![]() 上にあり, その
上にあり, その![]() 座標は4である。Bは
座標は4である。Bは![]() 上にあり, Dは
上にあり, Dは![]() 上にある。Cの
上にある。Cの![]() 座標は
座標は![]() であり, Cの
であり, Cの![]() 座標はBの
座標はBの![]() 座標より小さい。
座標より小さい。![]() ,
, ![]() の値をそれぞれ求めなさい。途中の式も含めた求め方も書くこと。ただし, 座標軸の1めもりの長さは1cmであるとする。
の値をそれぞれ求めなさい。途中の式も含めた求め方も書くこと。ただし, 座標軸の1めもりの長さは1cmであるとする。

答え
問題より, 正方形の一辺の長さは6とわかります。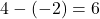
また,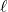 ,
, 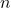 は平行なので,
は平行なので, 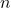 の式は
の式は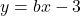 と置くことができます。
と置くことができます。
A, B, C, Dの座標を ,
, 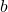 を用いて表すと,
を用いて表すと,
A(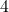 ,
, 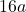 ), B(
), B(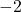 ,
, 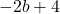 ), C(
), C(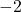 ,
, 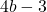 ), D(
), D(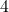 ,
, 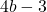 )
)
※A(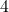 ,
, 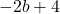 )としても可
)としても可
このとき, 辺BCの長さを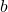 を用いて表すと,
を用いて表すと,
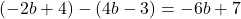
これが6と等しいので,
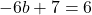
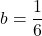
またA, Bの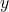 座標は等しいので,
座標は等しいので,

これに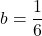 を代入し,
を代入し,
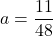
よって
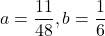 ・・・答え
・・・答え
また,
A, B, C, Dの座標を
A(
※A(
このとき, 辺BCの長さを
これが6と等しいので,
またA, Bの
これに
よって
 数樂管理人のブログ
数樂管理人のブログ 

