こんにちは。今回は関数の問題では頻出の解き方の問題です。解き方の流れをしっかりつかんでおきましょう。それではどうぞ。
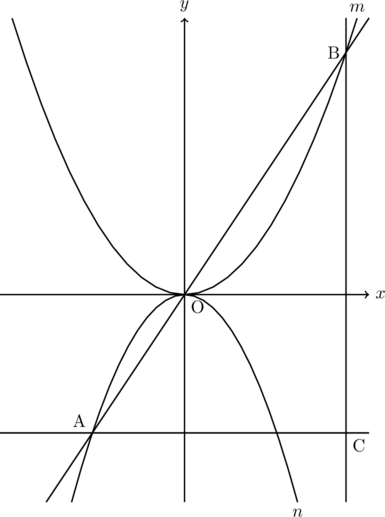
下の図において, ![]() は関数
は関数![]() (
(![]() は正の定数)のグラフを表し,
は正の定数)のグラフを表し, ![]() は関数
は関数![]() のグラフを表す。Aは
のグラフを表す。Aは![]() 上の点であり, その
上の点であり, その![]() 座標は負である。Bは, 直線AOと
座標は負である。Bは, 直線AOと![]() との交点のうちOと異なる点である。Cは, Aを通り
との交点のうちOと異なる点である。Cは, Aを通り![]() 軸に平行な直線とBを通り
軸に平行な直線とBを通り![]() 軸に平行な直線との交点である。Cの座標は
軸に平行な直線との交点である。Cの座標は![]() である。
である。![]() の値を求めなさい。
の値を求めなさい。

答え
(1) Cの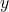 座標が
座標が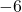 なので,
なので, 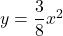 に代入して
に代入して
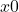 から
から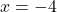 となり, Aの座標が
となり, Aの座標が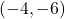 となる。
となる。
このことから直線ABの式が原点を通ることから, 直線ABを求めると,
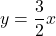 ・・・①となります。
・・・①となります。
点Bは直線①上にあり, Bの 座標はCの
座標はCの 座標と等しいので,
座標と等しいので,
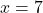 を①に代入して,
を①に代入して, 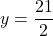 。
。
よってBの座標は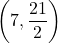 なので, これを
なので, これを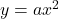 に代入して,
に代入して, 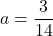
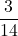 ・・・答え
・・・答え
このことから直線ABの式が原点を通ることから, 直線ABを求めると,
点Bは直線①上にあり, Bの
よってBの座標は
 数樂管理人のブログ
数樂管理人のブログ 

