中学数学：中3放物線の実践問題4

2020年8月6日

こんにちは。入試問題に近い問題を解いてみましょう。それではどうぞ。

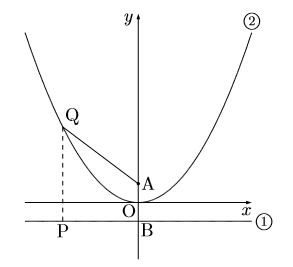
図のように, 直線 $y=-1\cdots$ ①, 関数 $y=\dfrac{1}{4}x^2\cdots$ ②のグラフがある。また, 点A $(0，1)$ , B $(0, -1)$ がある。点P, Qはそれぞれ, ①, ②のグラフ上にあり, P, Qの $x$ 座標は等しい。このとき次の問いに答えなさい。
(1) 関数 $y=\dfrac{1}{4}x^2$ について, $x$ の値が2から4まで増加するときの変化の割合を求めなさい。
(2) 点Pの $x$ 座標が $-6$ のとき, AQの長さを求めなさい。
(3) 点Pの $x$ 座標が $-4$ のとき, 4点P, Q, A, Rを結んでできる四角形がひし形になるようにRをとる。このときRの座標を求めなさい。
(4) (3)のとき点 $(0，2)$ を通ってひし形PQARの面積を二等分する直線の式を求めなさい。

プリントアウト用pdf

解答pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル