中学数学：中3放物線の実践問題7

2020年8月6日

こんにちは。今回は中3の放物線の実践問題をやってみましょう。それではどうぞ。

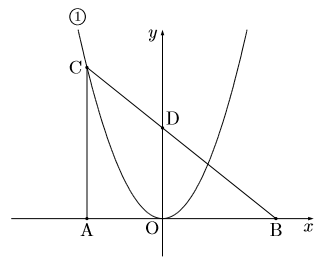
図で, 点Oは原点で, 点A, Bの座標はそれぞれ $(-4, 0)$ , $(6, 0)$ である。放物線①は関数 $y=\dfrac{1}{2}x^2$ のグラフである。点Aを通り, $y$ 軸に平行な直線をひき, 放物線①との交点をCとする。また, 線分BCと $y$ 軸の交点をDとする。このとき次の問いに答えなさい。
(1) 2点A, Bの距離を求めなさい。
(2) 直線CBの式を求めなさい。ただし, 変域は考えなくてよい。
(3) 関数 $y=\dfrac{1}{2}x^2$ で, $x$ の変域が $-2\leqq x\leqq1$ のとき, $y$ の変域を求めなさい。
(4) 線分AC上に点Pをとり, その $y$ 座標を $a$ とする。点Pと点Oを結ぶ。このとき, $\angle{\text{PCD}}=\angle{\text{DOP}}$ となる $a$ の値を求めなさい。

プリントアウト用pdf

解答pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル