中学数学：中3放物線の実践問題9

2020年8月7日

こんにちは。今回は中3の放物線の実践問題です。それではどうぞ。

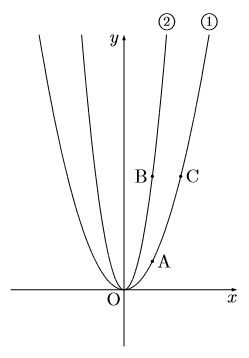
図で, 放物線①,②はそれぞれ関数 $y=x^2$ , $y=4x^2$ のグラフである。関数
$y=x^2$ のグラフ上に2点A, C, 関数 $y=4x^2$ のグラフ上に点Bがあり, 次の条件㋐～㋒を満たしている。
㋐ 3点A, B, Cのx座標は正の数。
㋑ 2点A, Bのx座標は等しい。
㋒ 2点B, Cのy座標は等しい。
このとき次の問いに答えなさい。
(1) 点Aの座標が $(1, 1)$ のとき, 他の2点の座標はB $(1, 4)$ , C $(2, 4)$ となる。このとき2点A, Cを通る直線の式を求めなさい。
(2) 点Aの $x$ 座標が3のとき, 点Cの座標を求めなさい。
(3) 点Aの $x$ 座標を $a$ とする。3点A, B, Cを結んでできる△ABCが二等辺三角形になるとき, $a$ の値を求めなさい。

プリントアウト用pdf

解答pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル