中学数学：攻略法：正負の数　初めての数学

こんにちは。中1の正負の数の初め辺りをすこし解説します。それではどうぞ。

数の範囲が広がるよ

まず中学生になって, 正負の数というものを学習します。これが数学における基本になりますので, ここでつまずくと, 以後学習する数学がつまらなくなる可能性が出てきますので, しっかり押さえてください。
特に計算はしっかりできるようにしておきましょう。
(1) では中学校の数学では何がどうなるのか見ていきましょう。
以下に数直線を書いてみます。数直線は数字が並んだ直線のことです。小学校のときに学習したのは, 0と0より大きな数の正の数というものです。中学校になったら, その数の範囲が変わります。学習する数の範囲が広がるのです。
それが0より小さい数の負の数というものです。身近な例でお話すると, 気温などがあるでしょう。12月の北海道のある日の気温が $-2.3^{\circ}$ Cとか。この $-$ をマイナスと呼び負の符号として扱うようになります。負の符号は基本的に省くことはできません。正の数には $+$ (プラス)という正の符号を付けて表すことがあります。正の符号は指示がある場合と, 与えられた問題に $+$ が付いていたりする場合を除けば省くことは可能です。
0は正の数, 負の数でもないので, 符号はありません。

まとめると,

同様に整数の範囲も変わります。整数とは分数と小数を除いたちょうどの数のことを言います。
これも正の整数, 0, 負の整数と3つに分類されます。また, 正の整数は自然数とも呼ばれますので, しっかり覚えておいてください。

数の分類

数の分類：次の8つの数字を各項目に分類しなさい。

$-2, +3.1, \dfrac13, -4.2, 5, +12, 0$

正の数を書きなさい。

$+3.1, \dfrac13, 5, +12$

負の数を書きなさい。

$-2, -4.2$

整数を書きなさい。

$-2, 5, +12, 0$

正の整数(自然数)を書きなさい。

$5, +12$

負の整数を書きなさい。

$-2$

正の数, 負の数でもない数を書きなさい。

$0$

こんな感じです。

また, 数直線に $\dfrac12$ や $-\dfrac13$ をどこか表すときは,

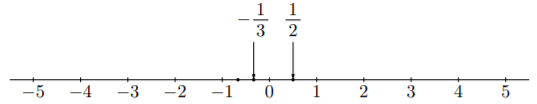
のように, 1目盛り1ならその間隔を2等分, 3等分して記すといいでしょう。

反対の意味を表すことができる

次に, この負の数を使ってどんなことができるのでしょうか。言葉の勉強をしていきましょう。
その前に反対の性質を表す言葉の学習をしておきましょう。(　)の中で対になっています。
(北, 南) , (東, 西) , (前, 後), (増える, 減る) , (増加, 減少) , (収入, 支出) , (利益, 損失), (足りる, 余る)
では本題に行きましょう。
まず, 簡単な暗号づくりから始めてみます。

東に3km進む, 西に4km進む

という言葉があるとします。
東と西はちょうど反対を表してることに気付きますか？ちょうど $+$ と $-$ も反対を表しています。この性質を用いて暗号が作れるんですね。

東に進むことを $+$ とすると, 西に進むことはそのちょうど反対になるので, $-$ を使って表すとこが可能になります。
したがって,

東に3km進む→ $+$ 3km
西に4km進む→ $-$ 4km

とできます。

10分前, 30分後　という前と後という反対の言葉も同じように扱うことが可能です。後を $+$ とすると, 前は $-$ になるので,

10分前→ $-10$ 分
30分後→ $+30$ 分

ここで, 単位は省けないので気を付けてください。こうやって, 自分で基準(どちらを $+$ にして, どちらを $-$ にするか)を決めておけば, いちいち西とか東とか書かなくていいんですね。

次にバカボン(知らないかもね？)のパパがよく言っていた, 反対の反対は賛成なのだ。という言葉のお遊びをやってみましょう。
言葉通りに反対のその反対は賛成になってしまうということですが, ピンと来ない方のために, コインを用意しました。
今表を向いているコインがあります。それを反対にすると裏になりますね。そしていま裏になったのを反対にすると表に戻りますね。
反対を2回繰り返すと物事は元に戻ってしまうという事実です。これを負の数を使って実現できるのです。

「 $+$ 500円の利益」という事実があったとします。これを損失という反対の性質を表す言葉を使って, 「 $+$ 500円の利益」と同じ意味の言葉をつくってみましょう。ただ, 前途したように, 同じ意味にするには反対を2回繰り返さないといけません。「 $+$ 500の損失」としたのでは意味が異なりますし, 1回しか反対にしていません。では, いま反対にした損失を反対にすると利益になって, 同じ意味(もとに戻る)になりますが, 損失という言葉を使っていないので, よくありません。
そこで, $+$ を $-$ と反対にすることで, 2回反対になることを実現するのです。つまり,

「 $+$ 500円の利益」 $=$ 「 $-$ 500円の損失」

とすれば反対を2回繰り返し, 同じ意味になることができます。符号と言葉の意味を反対にすることで, 反対を2回繰り返すということです。

「10分前」 $=$ 「 $-$ 10分後」}
「 $-3$ 大きい数」 $=$ 「 $+$ 3小さい数」

みたいな感じです。

絶対値

次に絶対値というものがでてきます。絶対値というものは数直線上の0からの距離のことをいいます。いま, 数直線上の0のところにC君がいて, A家が数直線上の $+$ 4のところ, B家が数直線上の $-$ 4のところにあったとします。C君はA家, B家のどちらに行くにしても距離は4になります。距離には正負の符号は関係ありません。
この場合, 正負の符号は東西のような方向の役割になります。このように $+4, -4$ から符号を取り除いた0からの距離である4のことを, $+4, -4$ の絶対値と呼びます。

つまり, $-4.3$ の絶対値は4.3, $+\dfrac13$ の絶対値は $\dfrac13$ , もともと符号の無い0の絶対値は0となります。
また, 正の数では絶対値が大きいほど数は大きくなり, 負の数では絶対値が大きくなるほど数は小さくなります。

絶対値が3より小さい数

$-2, -1, 0, 1, 2$

～よりというのは～を含みません。ですからこの場合3は含みません。
～未満も同じです。～は含みません。
絶対値が3以下の整数は何個ありますか。

$-3, -2, -1, 0, 1, 2, 3$

の7個。
～以下は～を含みます。この場合3は含みます。～以上も同じです。～を含みます。
つづいてこんな問題もあります。
次の数の中から絶対値が等しい数を書きなさい。

$-3, +0.5, -\dfrac12, -3.2, +3$

絶対値が等しい2つの数は,

$-3と+3, +0.5と-\dfrac12$

数の大小関係

数の大小
基本事項
(負の数) $<$ 0 $<$ (正の数)
$-2<3$ 　(負の数) $<$ (正の数)
$-3<-0.01$ 　(負の数どうしでは, 絶対値が小さい方が大きい)

正負の計算につながる思考

数直線を使って
(ア) 0より3小さい数を $-3$ とします。

(イ) 4より3小さい数はいくつですか。

4から小さい方へ3(4から左に3)進んだところのことですから1になります。

(ウ) $-3$ より5大きい数はいくつですか。

$-3$ より大きい方へ5( $-3$ より右に5)進んだところですから2になります。

(エ) $-1$ より $-3$ 大きい数はいくつでしょうか。

ポイントは普通日本語では $-3$ 大きいとは言いません。これを普通の日本語に直すと, $-3$ を3に直し, 大きいを小さいに変えて, 「 $-3$ 大きい」 $=$ 「3小さい」と直します。ですから, $-1$ より3小さい数を求めることと同じなので, $-1$ より小さい方へ3( $-1$ より左へ3)進んだところですから $-4$ になります。