emath講座：ソースコード：三角形の作図(2辺とその間の角が既知)

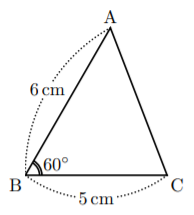
こんにちは。今回は2組の辺とその間の角がわかるときの三角形の作図です。

2組の辺とその間の角が分かっている三角形の作図。
今までのサンプルにはなかった, 三角形の決定方法です。

\tenretu{B(0,0)sw;C(5,0)se}
\Candk\B{6}\B{60}\AA\A
\Put\A[n]{A}
\Takakkei{\A\B\C}
\HenKo[*]<henkoh=3ex>\A\B{6\,cm}
\HenKo[*]<henkoh=3ex>\B\C{5\,cm}
\Kakukigou<2>\C\B\A(10pt,2pt){60$\Deg$}
\end{pszahyou*}

①の\Candk\B{6}\B{60}\AA\Aは, 点Bから方向角60の直線と, 点Bにコンパスをさして半径6の円を書いたときの交点をAA, Aとしますという意味です。
今回必要なのは, 点Aなので, 点Aに\PutでラベルAを張り付け, \Takakkeiで三角形ABCを書いています。
最後に必要な長さ, 角の大きさの表示して終わっています。

プリントアウト用pdf