これまでの知識を組み合わせると, おそらくほとんどできるようになったはずです。
例えば, 平行線と角。パート2
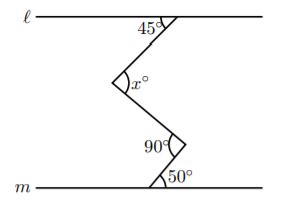
emath
\begin{pszahyou*}[ul=6mm,Ueyohaku=5mm](-1,8)(-1,6)
\tenretu*{A(0,6);B(8,6);C(0,0);D(8,0);P(4,0);Q(5,6)}
\Put\A[w]{$\ell$}
\Put\C[w]{$m$}
\Candk\P{2}\P{50}\RR\R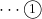 \kandk\R{-40}\Q{45}\S
\kandk\R{-40}\Q{45}\S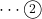 \Drawlines{\A\B;\C\D;\P\R\S\Q}
\Kakukigou<1>\D\P\R(10pt,3pt){$50\Deg$}
\Kakukigou<1>\S\R\P(-7pt,0pt){$90\Deg$}
\Kakukigou<1>\R\S\Q(7pt,0pt){$x\Deg$}
\Kakukigou<1>\A\Q\S(-7pt,-3pt){$45\Deg$}
\end{pszahyou*}
\Drawlines{\A\B;\C\D;\P\R\S\Q}
\Kakukigou<1>\D\P\R(10pt,3pt){$50\Deg$}
\Kakukigou<1>\S\R\P(-7pt,0pt){$90\Deg$}
\Kakukigou<1>\R\S\Q(7pt,0pt){$x\Deg$}
\Kakukigou<1>\A\Q\S(-7pt,-3pt){$45\Deg$}
\end{pszahyou*}どの点がどこにあるか, 示すと以下のようになります。
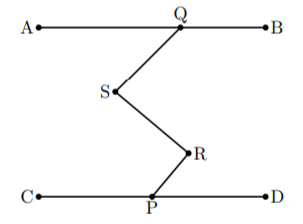
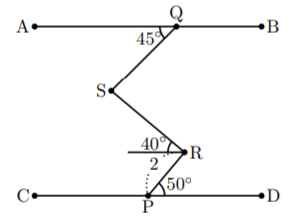
上のソースで何をやっているかというと, ①において, 点Pから方向角![]() の直線と点Pを中心とする半径2の円との交点をRR,Rとし,
の直線と点Pを中心とする半径2の円との交点をRR,Rとし,
②で, 点Rから方向角![]() の直線と点Qから方向角
の直線と点Qから方向角![]() の直線との交点をSとしています。\Drawlinesで平行線や角を描いて仕上げています。
の直線との交点をSとしています。\Drawlinesで平行線や角を描いて仕上げています。
 数樂管理人のブログ
数樂管理人のブログ 

