極座標\rtenretu
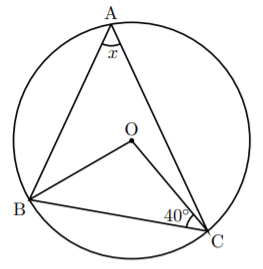
次のような円周角の問題について。
emath
\begin{pszahyou*}[ul=25mm,borderwidth=1em](-1,1)(-1,1)
\rtenretu{A(1,100)n;B(1,-150)sw;C(1,-50)se;O(0,0)n}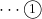 \Drawlines{\A\B\O\C\A;\B\C}
\En\O{1}
\Kakukigou\O\C\B<hankei=13pt>(-15pt,3pt)[l]{$40\Deg$}
\Kakukigou\B\A\C<hankei=13pt>(-2pt,-5pt)[l]{$x$}
\Kuromaru{\O}
\end{pszahyou*}
\Drawlines{\A\B\O\C\A;\B\C}
\En\O{1}
\Kakukigou\O\C\B<hankei=13pt>(-15pt,3pt)[l]{$40\Deg$}
\Kakukigou\B\A\C<hankei=13pt>(-2pt,-5pt)[l]{$x$}
\Kuromaru{\O}
\end{pszahyou*}すべては中心角。
上のソース①の点B, Cの意味するところを下図にしましました。
B![]() の意味するところは, 半径1の円周上の点で,
の意味するところは, 半径1の円周上の点で, ![]() の大きさが
の大きさが![]() となる点をBとするという意味。
となる点をBとするという意味。
同じく, C![]() は半径1の円周上の点で,
は半径1の円周上の点で, ![]() の大きさが
の大きさが![]() となる点をCとするという意味。このことで, 中心角である
となる点をCとするという意味。このことで, 中心角である![]() が
が![]() となる。あとは長い方の
となる。あとは長い方の![]() 上に点Aをとれば, その円周角は円周角の定理より,
上に点Aをとれば, その円周角は円周角の定理より, ![]() に設定できる。こうやって, 問題を作成していくといいでしょう。
に設定できる。こうやって, 問題を作成していくといいでしょう。
 数樂管理人のブログ
数樂管理人のブログ 

