中学・高校数学：箱ひげ図の描き方と見方

こんにちは。相城です。箱ひげ図について書いておこうと思います。
ヒストグラムは分布の形が分かりやすいが, 中央値などが分かりにくいのに対して, 箱ひげ図は, 中央値などが視覚的にわかるように工夫されており, 分布の広がりをわかりやすく表しています。

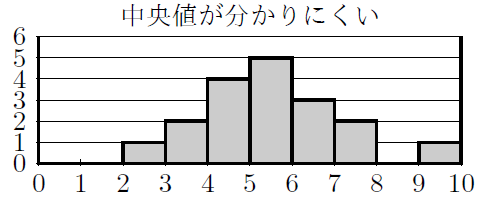
したがって, 箱ひげ図は2つ以上のデータを比べるに役立ちます。途中四分位偏差が出てきますが, 高校生の内容ですので, 中学生の方は飛ばしてくださって大丈夫です。

箱ひげ図

箱ひげ図は, 分布の広がりをわかりやすく表したもので, 以下のように書きます。

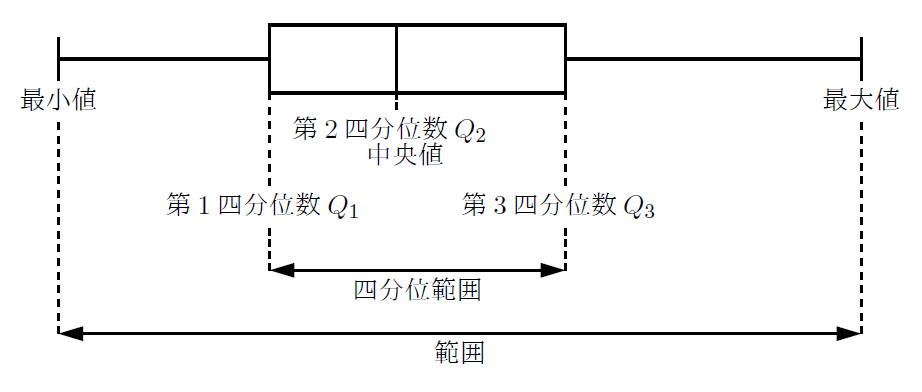
データの範囲は(最大値)－(最小値)で求まります。
四分位範囲は $Q_3$ (第3四分位数)－ $Q_1$ (第1四分位数)で求まります。
四分位偏差は $\dfrac{Q_3-Q_1}{2}$ , つまり, (四分位範囲) $\div$ 2で求まります。
各部を以下のようによぶこともあります。

四分位数の求め方

①データを小さい順に並べる。
②まず中央値 $Q_2$ (第2四分位数)を決める。
③中央値を境にデータを前半と後半に分けて, 第1四分位数 $Q_1$ (前半の中央値)・第3四分位数 $Q_3$ (後半の中央値)を決める。

四分位範囲とは

データの中に外れ値(極端に大きな値や極端に小さい値)があると, 範囲は影響を受けますが, 四分位範囲は影響をほとんど受けないので, そういった外れ値に強いのが四分位範囲の特徴です。四分位範囲もデータの散らばり具合を表すものなので, その値が大きいとデータの散らばり具合が大きいということになります。

具体的に描いてみる

具体的に描いてみます。
次のデータがあるとします。
1, 2, 3, 4, 5, 7, 9, 11, 12, 13, 15, 16, 17
このデータの中央値 $Q_2=$ 9
第1四分位数 $Q_1$ は $\dfrac{3+4}{2}=3.5$
第3四分位数 $Q_3$ は $\dfrac{13+15}{2}=14$
最小値は1, 最大値は17なので, 箱ひげ図は以下のようになります。

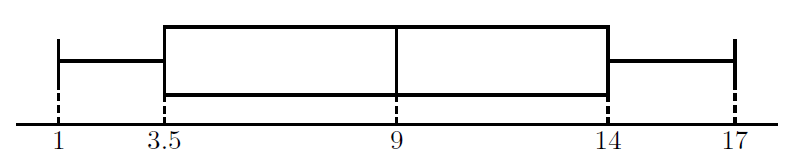
このデータからデータの範囲は $17-1=16$ ,
四分位範囲 $Q_3-Q_1$ は $14-3.5=10.5$ ,
四分位偏差は $\dfrac{Q_3-Q_1}{2}=\dfrac{10.5}{2}=5.25$
と分かります。

箱ひげ図に関する公式

①データの範囲＝(最大値)ー(最小値)
②四分位範囲＝ $Q_3-Q_1$
③四分位偏差＝ $\dfrac{Q_3-Q_1}{2}$

データの大体の割合

また, データの分布の割合を見ると最小値から $Q_1$ までは全体の約 $\dfrac{1}{4}$ (約25 $\%$ ), $Q_1$ ～ $Q_2$ も全体の約 $\dfrac{1}{4}$ (約25 $\%$ ), $Q_2$ ～ $Q_3$ も全体の約 $\dfrac{1}{4}$ (約25 $\%$ ), $Q_3$ ～最大値も全体の約 $\dfrac{1}{4}$ (約25 $\%$ )に構成されています。

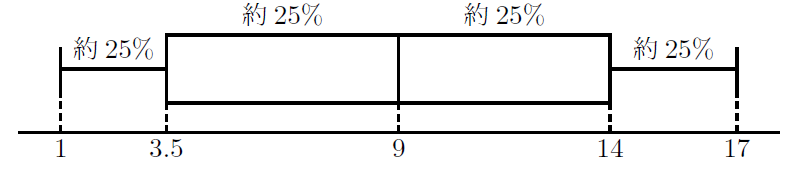
したがって, 9以上のデータは全体の約50 $\%$ になります。

大まかな分布が比較できる

ヒストグラムでデータを比較しようとすると, Aグループ, Bグループ, $\cdots$ という具合に多くの図が必要になります。また, この図では分布の変化が比べにくくなります。

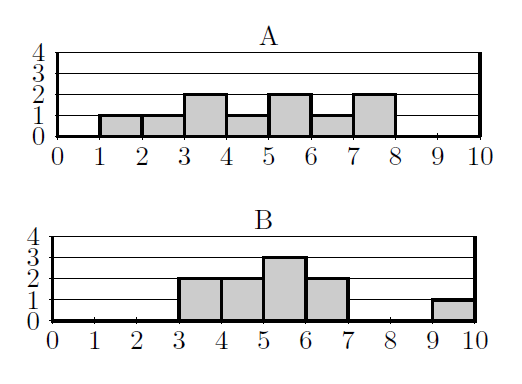
箱ひげ図にすると1つの図でデータの大まかな分布の様子が分かります。したがって, データの散らばり具合が比較しやすくなります。以下の例を見ていきましょう。

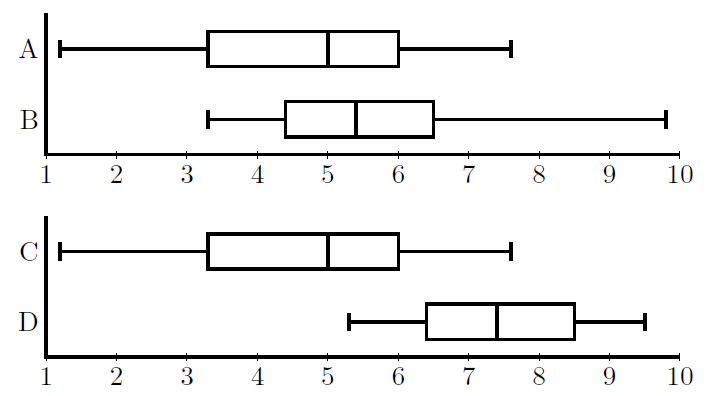
AとBを比較すると最小値から最大値までの長さがほぼ同じです。この場合, AとBのデータの散らばり具合はほぼ同じです。CとDを同じように比較すると, Cの方がデータの散らばり具合が大きいことが分かります。
A, Bでは中央値に大きな差はなく, Aでは中央値以下の約50％の人の散らばりが大きく, Bでは中央値以上の約50％の人の散らばりが大きいことが分かります。
C, Dでは, データの数値を見ると, DのデータはCの中央値より高い数値ににすべて分布していることが分かります。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル