こんにちは。相城です。今回は正弦定理について書いておきます。
正弦定理
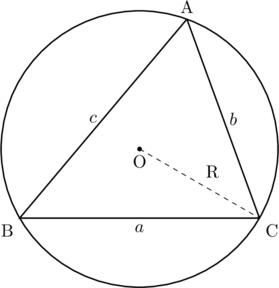
△ABCのBC![]() , CA
, CA![]() , AB
, AB![]() , △ABCの外接円の半径を
, △ABCの外接円の半径を![]() とするとき,
とするとき,
![]()
が成り立つ。これを正弦定理という。
パターン1:![]() が鋭角の場合(△ABCが鋭角三角形)
が鋭角の場合(△ABCが鋭角三角形)
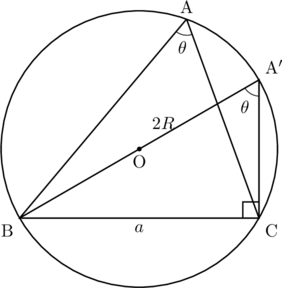
BA
これから
が成り立つ。
パターン2:![]() が鈍角の場合(△ABCが鈍角三角形)
が鈍角の場合(△ABCが鈍角三角形)
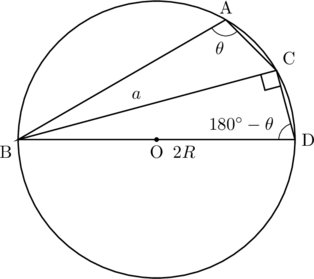
![]() が鈍角の場合, BDが円Oの直径
が鈍角の場合, BDが円Oの直径![]() となるように, 円周上に点Dをとり, 円Oに内接する四角形ABDCをつくって考える。
となるように, 円周上に点Dをとり, 円Oに内接する四角形ABDCをつくって考える。
このとき, 円に内接する四角形の内角の関係より, ![]() とすると,
とすると, ![]() である。また, 円周角の定理より,
である。また, 円周角の定理より, ![]() となる。このとき, BD
となる。このとき, BD![]() , BC
, BC![]() なので, △BDCに三角比を用いると,
なので, △BDCに三角比を用いると, ![]()
![]() であるから,
であるから, ![]()
よって,![]()
![]() なので,
なので, ![]()
![]() ,
, ![]() については鋭角なので, 前途したように成り立つことが知れているので,
については鋭角なので, 前途したように成り立つことが知れているので, ![]()
が成り立つ。
 TikZ:高校数学:正弦定理:余弦定理を用いた正弦定理の証明
TikZ:高校数学:正弦定理:余弦定理を用いた正弦定理の証明 数樂管理人のブログ
数樂管理人のブログ 

