高校数学：2次不等式の考え方について

こんにちは。相城です。今回は2次不等式について書いておきます。

二次不等式はグラフで考える

ある二次不等式 $ax^2+bx+c<0\ (a\neq 0)$ を解くと, $a(x-\alpha)(x-\beta)<0\ (\alpha<\beta)$ となった。
このとき, 不等式の解は $\alpha<x<\beta$ となるのはなぜでしょう。
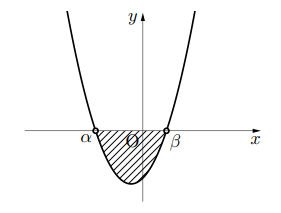
これは, 不等式の意味を読み取りましょう。左辺は0より小さいということです。このとき左辺を2次関数とみて, $y=ax^2+bx+c$ のグラフを書くと, 上の図のようになり, 0より小さい範囲(斜線部)は, $\alpha<x<\beta$ であり, これが不等式を満たす解になります。

同様に, $ax^2+bx+c>0\ (a\neq 0)$ を解くと, $a(x-\alpha)(x-\beta)>0\, (\alpha<\beta)$ となった。このとき, 不等式の解は $\alpha>x,\ x>\beta$ となるのはなぜでしょう。
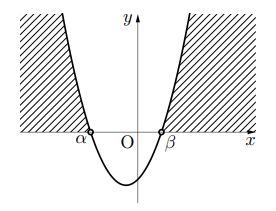
これは, 不等式の意味を読み取りましょう。左辺は0より大きいということです。このとき左辺を2次関数として, $y=ax^2+bx+c$ のグラフを書くと, 上の図のようになり, 0より大きい範囲(斜線部)は, $\alpha>x,\ x>\beta$ であり, これが不等式を満たす解になります。