こんにちは。相城です。今回はグラフの対称移動についてです。放物線を用いてお話ししていきます。
関数![]() を
を![]() 軸について対称移動する場合, 点
軸について対称移動する場合, 点![]() という座標は
という座標は![]() という座標に移動します。したがって,
という座標に移動します。したがって, ![]() 座標の符号がすべて反対になります。したがって関数
座標の符号がすべて反対になります。したがって関数![]() を
を![]() 軸に対称移動させると,
軸に対称移動させると, ![]() となり, これから
となり, これから![]() なります。
なります。
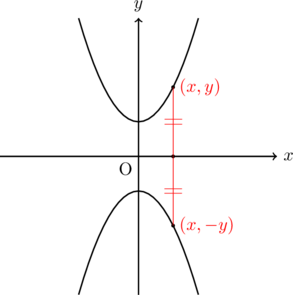
例: 関数![]() を
を![]() 軸に対称移動させなさい。
軸に対称移動させなさい。
答:![]() (右辺の符号を総変え)
(右辺の符号を総変え)![]() (答)
(答)
関数![]() を
を![]() 軸について対称移動する場合, 点
軸について対称移動する場合, 点![]() という座標は
という座標は![]() という座標に移動します。したがって,
という座標に移動します。したがって, ![]() 座標の符号がすべて反対になります。したがって関数
座標の符号がすべて反対になります。したがって関数![]() を
を![]() 軸に対称移動させると,
軸に対称移動させると, ![]() となります。
となります。
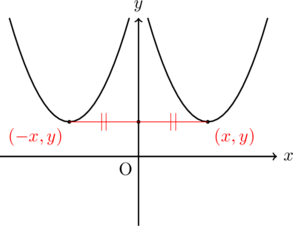
例: 関数![]() を
を![]() 軸に対称移動させなさい。
軸に対称移動させなさい。
答:![]() (
(![]() に
に![]() を代入)
を代入)![]() (符号が変わるのは
(符号が変わるのは![]() の奇数乗の部分だけ)
の奇数乗の部分だけ)![]() (答)
(答)
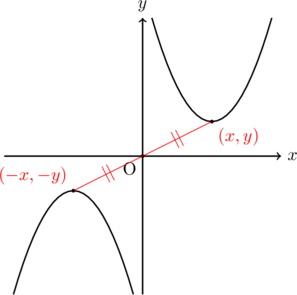
関数![]() を原点について対称移動する場合, 点
を原点について対称移動する場合, 点![]() という座標は
という座標は![]() という座標に移動します。したがって,
という座標に移動します。したがって, ![]() についての対称移動と
についての対称移動と![]() 軸についての対称移動の両方をすることになります。したがって関数
軸についての対称移動の両方をすることになります。したがって関数![]() を原点について称移動させると,
を原点について称移動させると, ![]() となります。
となります。
例: 関数![]() を原点について対称移動させなさい。
を原点について対称移動させなさい。
答:![]() (右辺の符号を総変え:
(右辺の符号を総変え:![]() 軸対称)
軸対称)![]() (
(![]() に
に![]() を代入・
を代入・![]() の奇数乗の部分だけ符号を変える:
の奇数乗の部分だけ符号を変える:![]() 軸対称)
軸対称)![]() (答)
(答)![]() 軸対称,
軸対称, ![]() 軸対称の順序はどちらが先でもよい。
軸対称の順序はどちらが先でもよい。
グラフの対称移動
![]()
![]() 軸対称
軸対称![]() ~の式の右辺の符号を総変え。
~の式の右辺の符号を総変え。![]()
![]() 軸対称
軸対称![]() ~の式で
~の式で![]() の奇数乗のところだけ符号を変える。
の奇数乗のところだけ符号を変える。![]() 原点対称
原点対称![]() の両方を1回ずつ行う。
の両方を1回ずつ行う。
 数樂管理人のブログ
数樂管理人のブログ 

