TikZ：高校数学：三角比から角度を求める

こんにちは。相城です。今回は三角比から角度を求めることを少し書いておこうと思います
高校1年生では扱う角度 $\theta$ が $0^{\circ}\leqq\theta\leqq180^{\circ}$ なので, その範囲で例題を追って書いておきます。

三角比：基本事項の確認

まず, 角度を求める前に, $\sin\theta$ , $\cos\theta$ , $\tan\theta$ は, 半径 $r$ の円(中心O)とその円周上の点P( $x$ , $y$ )を用いて次の式で得られます。
$\sin\theta=\dfrac{y}{r}$
$\cos\theta=\dfrac{x}{r}$
$\tan\theta=\dfrac{y}{x}$
ただし $\theta$ は動径(OP)と $x$ 軸の正の部分のなす角とします。
この考え方を使って $\theta$ を求めていきます。

例題を見ていこう

次の $\theta$ を求めなさい。ただし, $0^{\circ}\leqq\theta\leqq180^{\circ}$ とします。
① $\cos\theta=\dfrac{1}{\sqrt2}$
この場合, $\cos\theta$ は $\dfrac{x}{r}$ であるから, 半径 $r=\sqrt2$ の円を書いて, $x=1$ となる点をとると, 三平方の定理より $y$ 座標が1となるので, 以下の図のようになります。

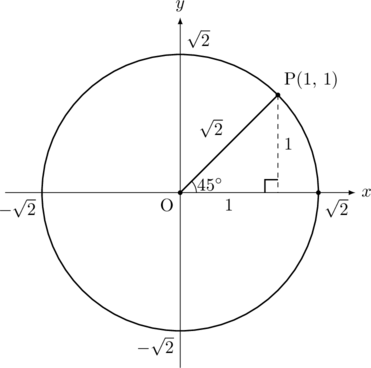
したがって, 求める $\theta$ は45 $^{\circ}$ となります。

知っておこう

$\cos\theta$ の値は $\dfrac{x}{r}$ で求まるように, $\cos\theta$ の符号は $x$ の符号で決まります。したがって, $x$ 座標の符号で $\theta$ が鋭角か鈍角か分かります。 $x>0$ のとき, $\cos\theta>0$ となり,この範囲では $\theta$ は鋭角になります。 $x<0$ のとき, $\cos\theta<0$ となり, この範囲では $\theta$ は鈍角になります。ちなみに $x=0$ のとき, $\cos\theta=0$ となり, $\theta$ は90 $^{\circ}$ (直角)になります。また, ここでは $\theta=0^{\circ}, 180^{\circ}$ では鋭角や鈍角にならないので無視して話をしています。

② $\sin\theta=\dfrac{\sqrt3}{2}$
この場合, $\sin\theta$ は $\dfrac{y}{r}$ であるから, 半径 $r=2$ の円を書いて, $y=\sqrt3$ となる点をとると, $\cos\theta$ とは異なり, そのような点は2つ(この2点は $y$ 軸について対称な関係)あります。このとき, 三平方の定理より, 残りの辺の長さは1になり, 以下の図のようになります。

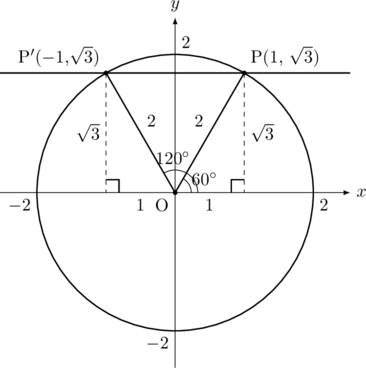
したがって, 求める $\theta$ は60 $^{\circ}$ , 120 $^{\circ}$ となります。

知っておこう

$\sin\theta$ の値は円周上の1つの点と, $y$ 軸対称な点(円周上の1点から真横( $x$ 軸に平行)に引いた直線と円周との交点)の2点で, 同じ値(半径と $y$ 座標が同じだから)になります。ですから $\sin\theta$ を満たす $\theta$ は鋭角と鈍角2つ存在することになります。ちなみに高校1年生のときは $\sin\theta\geqq0$ です。理由は扱う $\theta$ の範囲が $0^{\circ}\leqq\theta\leqq180^{\circ}\ (y\geqq0)$ だからです。

③ $\tan\theta=-\sqrt3$
この場合, $\tan\theta$ は $\dfrac{y}{x}$ で, $\theta$ の範囲から $(y\geqq0)$ なので, $-\sqrt3=\dfrac{\sqrt3}{-1}=\dfrac{y}{x}$ となる。したがって, $x=-1$ , $y=\sqrt3$ とすると, 三平方の定理より, 直角三角形の斜辺は2となるので, 以下の図のように, 半径2の円になります。 $\theta$ は鈍角のみになります。

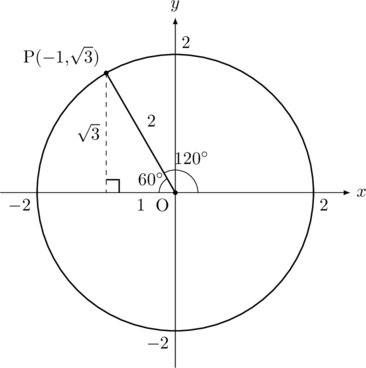
したがって, 求める $\theta$ は120 $^{\circ}$ となります。

知っておこう

$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ において, $0\leqq\theta\leqq180^{\circ}$ の範囲では $\sin\theta\geqq0$ なので, $\tan\theta$ の符号は $\cos\theta$ の符号で決まります。今回 $\tan\theta<0$ なので, $\cos\theta$ の値は $\cos\theta<0$ となるので, $\theta$ は鈍角1つのみになります。また, お気づきかもしれませんが, $-\sqrt3=\dfrac{-\sqrt3}{1}=\dfrac{y}{x}$ の場合, つまり, $x=1$ , $y=-\sqrt3$ のときも答えとして成立するのですが, $y<0$ となる場合は, $0^{\circ}\leqq\theta\leqq180^{\circ}$ の範囲を超えるので, 扱いは高校2年生からになります。

高校2年生で習うこと

知っておこう

前途したように, $\sin\theta$ の値は円周上の1点とそれと $y$ 軸対称な2点で, 同じ値(半径と $y$ 座標が同じだから)になります。これと同じ考え方を使って $\cos\theta$ の値でも同様のことが言えます。 $\cos\theta$ の値は円周上の1点と $x$ 軸対称(円周上の1点から真縦( $y$ 軸に平行)に引いた直線と円周との交点)の2点で, 同じ値(半径と $x$ 座標が同じだから)になります。ちなみに, $\tan\theta$ の値は円周上の1点と, 原点について対称な点の2点で, 同じ値を取ります。ただし, これらは $y<0$ となる範囲( $180^{\circ}<\theta<360^{\circ}$ の範囲)を含んでいるので, これを扱うのは高校2年生になってからになります。

三角比：基本事項の確認

例題を見ていこう

高校2年生で習うこと

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル