こんにちは。相城です。今回は三角形の内角の二等分線の比について書いておきます。
内角の二等分線の比の公式
内角の二等分線の比の公式
例題をやってみよう
実際問題をやってみよう。
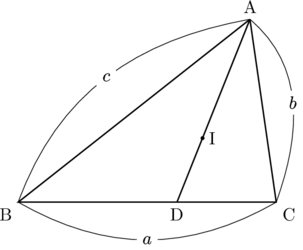
下の図の△ABCにおいて内心をIとし, AIの延長線と辺BCとの交点をDとする。このとき, BDの長さと, AI : IDの比を求めなさい。
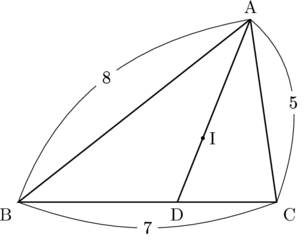
【解説】
内心Iは三角形の内角の二等分線の交点なので, 直線AIは
したがって,
AB : AC
AB : AC
BD : DC
よって,
BD
BIもまた,
AI : ID
AI : ID
よって, BD
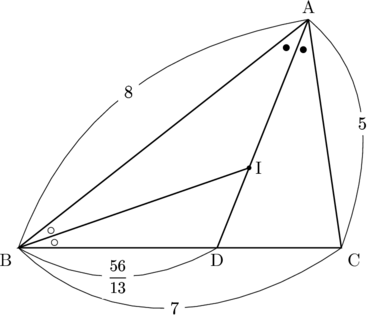
公式にしてみよう
公式化してみよう
AI : IDを公式化してみよう。Iは△ABCの内心, DはAIの延長線とBCとの交点
BD : DC
なので, BD
BD
AI : ID
AI : ID
AI : ID
という公式が得られます。
実際上の例題で,
AI : ID
となります。
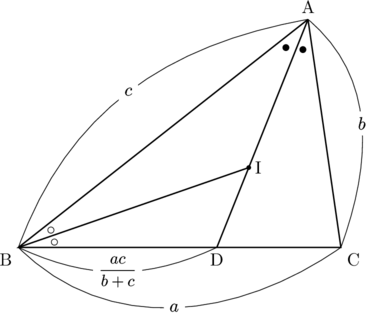
AI : IDの公式
△ABC(BC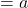 , CA
, CA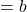 , AB
, AB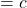 )の内心をIとし, 線分AIの延長線と辺BCとの交点をDとするとき,
)の内心をIとし, 線分AIの延長線と辺BCとの交点をDとするとき,
AI : ID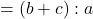
AI : ID
 数樂管理人のブログ
数樂管理人のブログ