こんにちは。相城です。今回は円に内接する四角形の問題に取り組んでみたいと思います。四角形の1つの内角が分かる場合をやってみましょう。
円に内接する四角形で, AB![]() 2, BC
2, BC![]() 5, CD
5, CD![]() 3,
3, ![]() のとき, 次のものを求めよ。
のとき, 次のものを求めよ。
(1) ![]() の大きさ
の大きさ
(2) BDの長さ
(3) 四角形ABCDの面積![]()
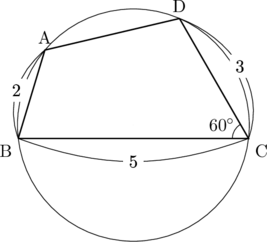
【解説】
(1) 円に内接する四角形の対角の和は180![]() なので,
なので, ![]()
(2) △BCDに余弦定理を用いると,
BD![]()
![]()
![]()
![]() なので,
なので,
BD![]()
(3) 四角形の面積は2つの三角形の面積の和として考えることが多い。
今回も, 四角形ABCDは△ABD![]() △BCDで求める。
△BCDで求める。
三角形の面積を求めるためには, 2辺とその間のその間の角が求まればよいので, (2)の結果を用いて, △ABDで余弦定理を用いて, ADを求める。
AD![]() とおくと,
とおくと, ![]()
![]()
![]()
![]()
![]()
![]() より,
より, ![]()
よって, AD![]()
したがって, △ABD, △BCDの面積は次のようになります。
△ABD![]()
△BCD![]()
よって, 四角形ABCDの面積![]() は,
は, ![]()
流れをつかんでおこう
- 角の大きさが分かる場合は, 余弦定理で他の辺を求めて2辺とその間が分かるように導いていく。
- 四角形の面積は2つの三角形の面積の和と考え, 三角形の面積を
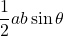 で求めて, 加える。
で求めて, 加える。
 数樂管理人のブログ
数樂管理人のブログ 

