TikZ：高校数学：四角形の面積

こんにちは。今回は普通の四角形の面積に関してです。4辺と1つの内角が分かっているときを書いておきます。

例題をやってみよう

AB $=$ 5, BC $=$ 6, CD $=$ 3, DA $=$ 4, $\cos A=\dfrac{7}{20}$ の四角形ABCDがあります。このとき, 次のものを求めよ。
(1) $\sin A$ の値
(2) BDの長さ
(3) 四角形ABCDの面積 $S$

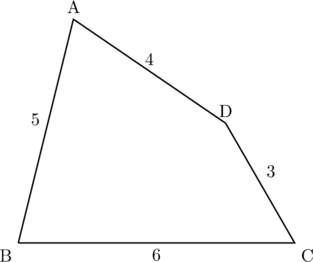
【解説】
(1) $\cos A$ の値を $\sin^2 A+\cos^2 A=1$ に代入すると,
$\sin^2 A+\left(\dfrac{7}{20}\right)^2=1$
$\sin^2 A=1-\dfrac{49}{20^2}$
$=\dfrac{351}{20^2}$
$\sin A>0$ より,
$\sin A=\dfrac{3\sqrt{19}}{20}$
(2) △ABDで余弦定理を用いると,
BD $^2=5^2+4^2-2\cdot5\cdot4\cdot\cos A$
$=25+16-2\cdot5\cdot4\cdot\dfrac{7}{20}$
$=27$
BD $>0$ なので,
BD $=3\sqrt3$
(3) 四角形ABCD $(S)=$ △ABD $(T)+$ △BCD $(U)$ として求める。
△ABDの面積 $T$
$T=\dfrac12\cdot5\cdot4\cdot\sin A$
$=\dfrac12\cdot5\cdot4\cdot\dfrac{3\sqrt{19}}{20}$
より,
$T=\dfrac{3\sqrt{19}}{2}$
△BCDは余弦定理で $\cos C$ の値を求めると,
$\cos C=\dfrac{6^2+3^2-(3\sqrt3)^2}{2\cdot6\cdot3}$
から,
$\cos C=\dfrac12$
よって
$C=60^{\circ}$
したがって, △BCDの面積 $U$ は,
$U=\dfrac12\cdot6\cdot3\cdot\sin60^{\circ}$
より,
$U=\dfrac{9\sqrt3}{2}$
以上より, 求める四角形ABCDの面積 $S$ は,
$S=T+U$
$S=\dfrac{3\sqrt{19}}{2}+\dfrac{9\sqrt3}{2}$
となります。

流れをつかんでおこう

四角形の内角が1つ分かっているときは, その角と向かい合う対角線で四角形を三角形2つに分割して考える。誘導があればそれに乗っかるとよい。
1つの三角形の面積は, 分かっている角の 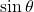$\sin\theta$ の値を求めることで, 2辺とその間の角で, 三角形の面積を求める。
もう1つの三角形は前途した角で余弦定理を用いて対角線の長さを求め, 3辺が分かったところで, 余弦定理で, 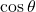$\cos\theta$ の値を求め, それから, 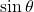$\sin\theta$ を求めることで, 同様に2辺とその間の角に持ち込んで, 三角形の面積を求める。
四角形の面積は, 上の2つの三角形の面積の和として求める。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル