TikZ：中学数学：攻略法：平行四辺形と角の二等分線

こんにちは。相城です。今回は平行四辺形と角の二等分線についてです。応用問題でも出題されますので, 知識として知っておいて問題ないでしょう。それではどうぞ。

例題を見てみよう

以下のような例題を用意しました。

四角形ABCDは平行四辺形で, AB $=$ 8cm, AD $=$ 5cmで, Fは辺CD上の点である。BCの延長線と, AFの延長線が交わる点をEとするとき, 線分AEは $\angle{\text{BAD}}$ の二等分線である。このとき, DFの長さとAF : EFを求めなさい。

二等辺三角形が隠れてる

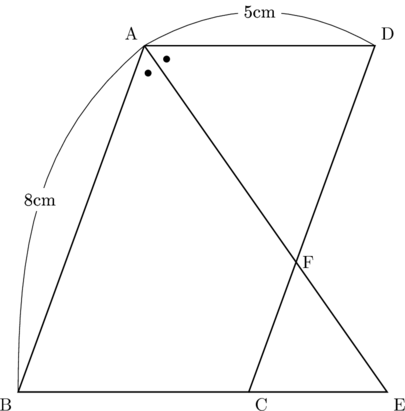
さて, この問題を解くカギは二等辺三角形を見つけることにあります。皆さんはこの図形の中に二等辺三角形をいくつ見つけることができたでしょうか。例題の図には分かりやすいように $\bullet$ を付けていますが, 普通はついていないことが多いので, 印がついていないときは自分でつけてください。以下の図で, 印の付いた角はみな同じ角の大きさになります。
印の付いた角が同じになる理由を示すと, $\angle{\text{CFE}}$ は $\angle{\text{BAE}}$ の同位角, $\angle{\text{AEB}}$ は $\angle{\text{DAE}}$ の錯角, $\angle{\text{AFD}}$ と $\angle{\text{CFE}}$ は対頂角だからです。
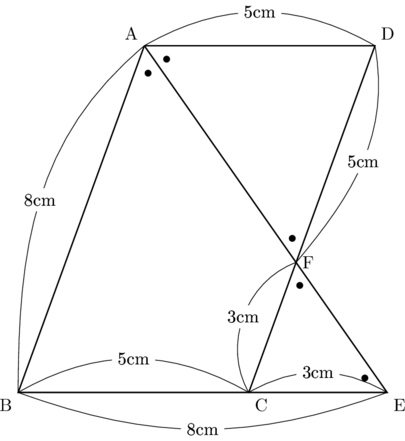
したがって, △ADF, △CFE, △ABEは二等辺三角形になります。このことから, DF $=$ 5cmであることが分かります。これでAF : EFを求めるのに十分ですが, あえて違う角度からAF : EFを求めることにします。△ABEが二等辺三角形なので, BE $=$ 8cmとなり, BC $=$ 5cmなので, CE $=$ 3cmであることが分かります。したがって, △ADF∽△ECFであることから, AF : EF $=$ AD : EC $=$ 5 : 3と分かります。
以上より, 求める答えは,
DF $=$ 5cm, AF : EF $=$ 5 : 3